Teil B, Gruppe 2

Die Theatergruppe einer Mittelschule druckt für das Bühnenbild einfache achsensymmetrische Blumen (siehe Szizze) auf Stoff.

Berechne den Flächeninhalt einer solchen Blume.

Punkte: 5

Für diese Aufgabe benötigst Du folgendes Grundwissen: Satz des Pythagoras

Außerdem benötigst du die Flächenformeln für Dreiecke, Rechtecke und Kreise.

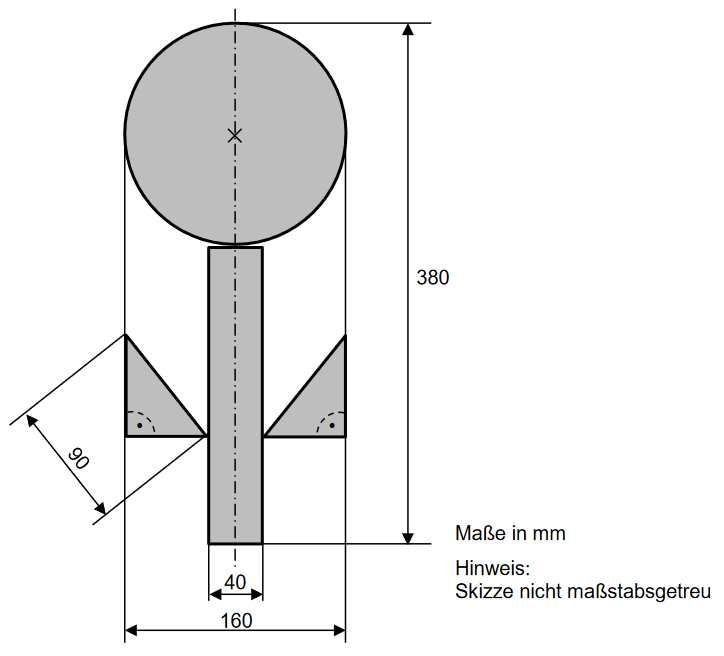
Berechne nacheinander den Flächeninhalt der Teilfiguren und addiere am Schluss.

Kreis

Aus der Skizze kannst du ablesen, dass der Kreis einen Durchmesser von $160$ hat. Teile diesen Wert durch 2, um deinen Radius zu erhalten.

$160 𝕞 𝕞 : 2 = 80 𝕞 𝕞$ $\Rightarrow$ Der Radius beträgt also $80 𝕞 𝕞$ .

Nun kannst du den Flächeninhalt des Kreises mit der Formel $A_{K} = π \cdot r^{2}$ berechnen.

$A_{K} = π \cdot r^{2} = 3,14 \cdot (80 𝐦 𝐦)^{2} = 3,14 \cdot 80 𝐦 𝐦 \cdot 80 𝐦 𝐦 = 20096^{} {𝐦 𝐦}^{2}$ $\Rightarrow$ Die Fläche des Kreises beträgt $20096 {𝐦 𝐦}^{2}$ .

Dreieck

Da es sich um eine achsensymmetrische Figur handelt, müssen beide Dreiecke gleich groß sein. Eine Seite (die Hypotenuse) des Dreiecks ist gegeben ( $90 𝕞 𝕞$ ). Die zweite Seite (a), eine der Katheten, kannst du mit Hilfe der Angaben berechnen.

$160 𝕞 𝕞 - 40 𝕞 𝕞 = 120 𝕞 𝕞$ $120 𝕞 𝕞 : 2 = 60 𝕞 𝕞$ $\Rightarrow$ Die Seite a des Dreiecks beträgt $60 𝕞 𝕞$ .

Die letzte Seite (b) kannst du nun mit Hilfe des Satz des Pythagoras berechnen.

$a^{2} + b^{2} = c^{2}$

Setze die Werte für $a$ und $c$ ein.

$(60 𝕞 𝕞)^{2} + b^{2} = (90 𝕞 𝕞)^{2} | - (60 𝕞 𝕞)^{2}$

Stelle nach $b^{2}$ um.

$b^{2} = (90 𝕞 𝕞)^{2} - (60 𝕞 𝕞)^{2}$

Ziehe die Wurzel

$b = \sqrt{4500 {𝕞 𝕞}^{2}} \approx 67,1 𝕞 𝕞$

Berechne nun den Flächeninhalt des Dreiecks mit der Formel $A = 0,5 \cdot a \cdot h$ . In diesem Fall entspricht die Höhe h der Seite b, da bei C rechter Winkel ist. Außerdem musst du dein Ergebnis noch mit $2$ muliplizieren, um die Fläche beider Dreiecke zu erhalten.

$A = 0,5 \cdot 60 𝕞 𝕞 \cdot 67,1 𝕞 𝕞 = 2013 {𝕞 𝕞}^{2}$ $2013 {𝕞 𝕞}^{2} \cdot 2 = 4026 {𝕞 𝕞}^{2}$ $\Rightarrow$ Beide Dreiecke zusammen haben eine Fläche von $4026 {𝕞 𝕞}^{2}$ .

Rechteck

Zulezt musst du die Fläche des Rechtecks berechnen. Hierbei hast du eine Länge (a) gegeben ( $40 𝕞 𝕞$ ). Die 2. Länge (b) kannst du berechnen, indem du den Durchmesser des Kreises ( $160 𝕞 𝕞$ ) von der Länge der gesammten Figur ( $380 𝕞 𝕞$ ) abziehst.

$380 𝕞 𝕞 - 160 𝕞 𝕞 = 220 𝕞 𝕞$

$\Rightarrow$ Die Seite b ist $220 𝕞 𝕞$ lang.

Mit diesen Werten und der Formel $A = a \cdot b$ kannst du nun den Flächeninhalt des Rechtecks berechnen.

$A = 40 𝕞 𝕞 \cdot 220 𝕞 𝕞 = 8800 𝕞 𝕞^{𝟚}$

$\Rightarrow$ Die Fläche des Rechtecks beträgt $8800 {𝕞 𝕞}^{2}$ .

Gesamtfläche

Um nun die Fläche der gesammten Figur zu erhalten, musst du alle Flächeninhalte miteinander addieren.

$A = 20096 {𝕞 𝕞}^{2} + 4026 {𝕞 𝕞}^{2} + 8800 {𝕞 𝕞}^{2} = 32922 {𝕞 𝕞}^{2}$ $\Rightarrow$ Insgesammt hat die Figur einen Flächeninhalt von $32922 {𝕞 𝕞}^{2}$ .

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das? serlo.org