Aufgaben zu Tangenten an Parabeln
Die Tangenten von einem Punkt der Symmetrieachse der Parabel an die Parabel stehen aufeinander senkrecht. Berechne die Berührpunkte und die Gleichungen der Tangenten.
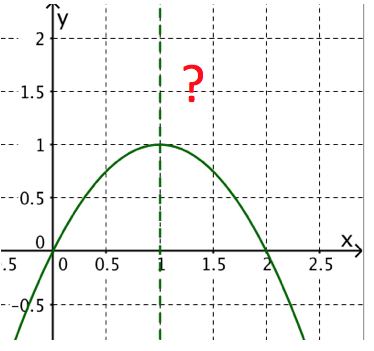
Die Tangenten von einem Punkt der Symmetrieachse der Parabel an die Parabel stehen aufeinander senkrecht. Berechne die Berührpunkte und die Gleichungen der Tangenten.



