Gemischte Aufgaben zu Funktionen

Betrachte die Funktion $f (x) = \frac{\exp (x) - 4}{\exp (x) + 4}$ . Der Graph der Funktion ist $G_{f}$ und ihr Definitionsbereich $D_{f} = ℝ$ .

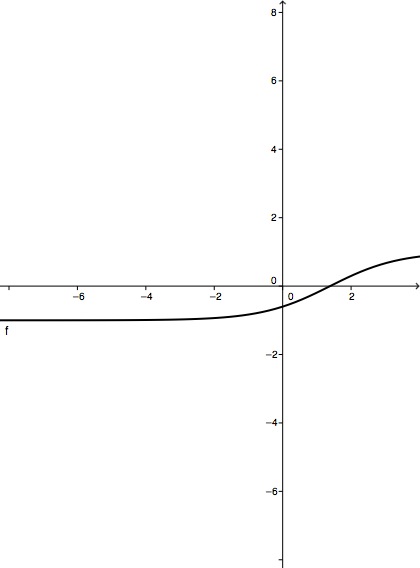
Berechne die Koordinaten des Schnittpunkts $S$ von $G_{f}$ mit der y-Achse.

Berechne anschließend die Koordinaten des Schnittpunkts $S$ von $G_{f}$ mit der x-Achse.

Bestimme das Verhalten von $f (x)$ für $x \to \infty$ und $x \to - \infty$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: asymptotische Verhalten der Funktion
Hinweis: Zur Bestimmung des Grenzwerts für $x \to \infty$ kann z.B. zunächst im Zähler und im Nenner $e^{x}$ ausgeklammert werden.
Betrachte das asymptotische Verhalten der Funktion
Bestimme das Verhalten für $x \to \infty$ .
$\lim_{x \to \infty} \frac{e^{x} - 4}{e^{x} + 4}$
Klammere im Zähler und im Nenner je $e^{x}$ aus.
$= \lim_{x \to \infty} \frac{e^{x} (1 - 4 \cdot e^{- x})}{e^{x} (1 + 4 \cdot e^{- x})}$
Kürze $e^{x}$ .
$= \lim_{x \to \infty} \frac{1 - 4 \cdot e^{- x}}{1 + 4 \cdot e^{- x}}$
Führe die Grenzwertbetrachtung durch. Dabei wird $\lim_{x \to \infty} e^{- x} = 0$ .
$= \frac{1 - 0}{1 + 0} = 1$
Bestimme das Verhalten für $x \to - \infty$ .
$\lim_{x \to - \infty} \frac{e^{x} - 4}{e^{x} + 4}$
Führe die Grenzwertbetrachtung durch. Dabei wird $\lim_{x \to - \infty} e^{x} = 0$ .
= $\frac{0 - 4}{0 + 4}$
Forme um.
= $\frac{- 4}{4} = - 1$
Untersuche das Monotonieverhalten von $G_{f}$ mit Hilfe der ersten Ableitung von $f$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Hinweis zur Kontrolle:
Die erste Ableitung lautet $f^{'} (x) = 8 \cdot \frac{\exp (x)}{(\exp (x) + 4)^{2}}$ .
Berechne die Ableitung
Bilde die erste Ableitung der Funktion.
$f^{'} (x) = {(\frac{e^{x} - 4}{e^{x} + 4})}^{'}$
Wende die Quotientenregel an.
$= \frac{e^{x} (e^{x} + 4) - e^{x} (e^{x} - 4)}{(e^{x} + 4)^{2}}$
Löse die Klammer im Zähler auf.
$= \frac{e^{2 x} + 4 e^{x} - e^{2 x} + 4 e^{x}}{(e^{x} + 4)^{2}}$
Vereinfache den Zähler.
$= \frac{8 e^{x}}{(e^{x} + 4)^{2}}$
Bestimme das Monotonieverhalten
Da die erste Ableitung der Funktion $f^{'} (x) = \frac{8 e^{x}}{(e^{x} + 4)^{2}}$ für alle x-Werte größer als Null ist, ist die Funktion streng monoton steigend.
Dass $f^{'} (x) = \frac{8 e^{x}}{(e^{x} + 4)^{2}} > 0$ für alle x-Werte gilt, sieht man an der Exponentialfunktion im Zähler und dem quadratischen Ausdruck im Nenner. Beide sind stets größer als 0.

W (ln 4 | 0) ist der einzige Wendepunkt von $G_{f}$ . Zeige, dass die Gerade n mit der Gleichung $y = - x + \ln 4$ durch W verläuft und auf der Wendetangente senkrecht steht.

Verschiebe $G_{f}$ um ln 4 nach links, um den Graphen $G_{f^{*}}$ zu erhalten und gib $f^{*}$ an. Zeige, dass $G_{f^{*}}$ punktsymmetrisch zum Ursprung ist. Welche Bedeutung hat in diesem Fall der Punkt W für $G_{f}$ ?

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org

$\frac{e^{x} - 4}{e^{x} + 4}$	$=$	$0$
	↓	Multipliziere $e^{x} + 4$ auf beiden Seiten. Da die Exponentialfunktion nie negativ wird, kannst auf beiden Seiten den Ausdruck multiplizieren.
$e^{x} - 4$	$=$	$0$
	↓	Bringe 4 auf die andere Seite.
$e^{x}$	$=$	$4$
	↓	Wende den Logarithmus als Umkehrfunktion der Exponentialfunktion an.
$x$	$=$	$\ln 4$
	↓	Die y-Koordinate der Nullstelle ist 0. Gib den Schnittpunkt an.
$S_{x}$	$=$	$(\ln 4 \| 0)$
	$=$
	$=$

$f (0)$	$=$	$\frac{e^{0} - 4}{e^{0} + 4}$
	$=$	$\frac{1 - 4}{1 + 4}$
	↓	Führe die Subtraktion und die Addition aus.
	$=$	$- \frac{3}{5}$
	↓	Gib den Schnittpunkt an.
$S_{y}$	$=$	$(0 \| - \frac{3}{5})$

$W : y$	$=$	$m_{W} \cdot x + t$
	↓	Berechne die Steigung der Wendetangente über die Steigung der Funktion im Wendepunkt W (ln 4 \| 0).
$m_{W}$	$=$	$f ´ (\ln 4)$
	$=$	$8 \cdot \frac{e^{\ln 4}}{(e^{\ln 4} + 4)^{2}}$
	↓	Vereinfache indem du verwendest, dass der Logarithmus die Umkehrfunktion der Exponentialfunktion ist.
	$=$	$8 \cdot \frac{4}{(4 + 4)^{2}}$
	$=$	$\frac{32}{64}$
	$=$	$\frac{1}{2}$
	↓	Bestimme nun den y-Achsenabschnitt der Wendetangente, indem du forderst, dass diese auch durch den Wendepunkt gehen muss.

Gemischte Aufgaben zu Funktionen

Schnittpunkt mit der x-Achse berechnen

Schnittpunkt mit der y-Achse berechnen

Betrachte das asymptotische Verhalten der Funktion

Berechne die Ableitung

Bestimme das Monotonieverhalten

Zeige, dass die Gerade n durch W verläuft

Bestimme die Wendetangente

Zeige, dass die Wendetangente senkrecht auf der Geraden n steht