B I

Die Punkte $A$ und $B$ legen die Gerade $g$ fest, die Punkte $C_k$ liegen auf der Geraden $h$. Geben Sie jeweils eine Gleichung der beiden Geraden an und untersuchen Sie die gegenseitige Lage der beiden Geraden.

Für die folgenden Teilaufgaben gilt $k=-3$. Es ergibt sich $C_{-3}-(\text{–}3|\text{–}5|3)$.

(1) Die Punkte $A,B$ und $C_{-3}$ legen die Ebene $E$ fest. Bestimmen Sie je eine Gleichung der Ebene $E$ in Parameter- und Koordinatenform.

[ mögliches Teilergebnis: $E:x_1+x_2+3x_3-1=0$]

(2) Untersuchen Sie die Lagebeziehung der Ebene $E$ mit der Ebene $F:\overrightarrow{x}=\left(\begin{array}{c}2\\ 2\\ -1\end{array}\right)+r\cdot \left(\begin{array}{c}-5\\ -7\\ 4\end{array}\right)+t\cdot \left(\begin{array}{c}1\\ 3\\ 6\end{array}\right)$ mit $r,t\in ℝ$ und bestimmen Sie gegebenenfalls eine Gleichung der Schnittgeraden.

(3) Die Punkte $A,B,C_{-3}$ und $D(3|5|5)$ legen ein Tetraeder fest (siehe Skizze).

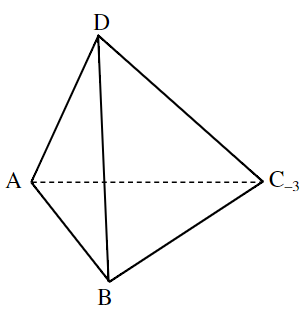
Spiegelt man den Punkt $C_3$ am Punkt $D$, so erhält man den Punkt $C_{-3}^{\ast }$. Berechnen Sie die Koordinaten des Punktes $C_{-3}^{\ast }$.

(4) Der Punkt $C_{-3}^{\ast }$ liegt in der Ebene $F$ (Nachweis nicht erforderlich). Eine der Seitenflächen des Tetraeders liegt ganz in der Ebene $F$. Entscheiden Sie, welche der Flächen das ist und begründen Sie Ihre Entscheidung.

(5) Der Punkt $S(-{\displaystyle \frac{1}{3}}|-{\displaystyle \frac{5}{3}}|1)$ ist Schwerpunkt des Dreiecks $AB{C}_{-3}$, der Punkt $M$ ist Mittelpunkt der Kante $\overline{AB}$und der Punkt $N$ ist Mittelpunkt der Kante $\overline{D{C}_{-3}}$. Die Gerade $MN$ und die Gerade $DS$ schneiden sich im Punkt $P$. Berechnen Sie Koordinaten des Punktes $P$.