Anwendungsaufgaben der Differential- und Integralrechnung

Gegeben sind die Funktion $h(x)=2x-7$ und der Punkt $A(1|2)$.

Ansatz für die lineare Funktion $g(x)$: $g(x)=mx+n.$

(Anmerkung: Das absolute Glied heißt hier $n$ um Verwechslungen mit der quadratischen Funktion zu vermeiden.)

Quadratischer Ansatz für die Funktion $f(x)$: $f(x)=a{x}^2+bx+c$.

Die erste Ableitung von $f(x)$ lautet: $f^{\prime }(x)=2ax+b$.

Die erste Ableitung von $g(x)$ lautet: $g^{\prime }(x)=m$.

Die erste Ableitung von $h(x)$ lautet: $h^{\prime }(x)=2$.

1. versatzfrei: $f(1)=g(1)=2$ $\Rightarrow$ $2=a+b+c$ $(1)$ $f(6)=h(6)=5$ $\Rightarrow$ $5=36a+6b+c$ $(2)$

2. knickfrei: $f^{\prime }(1)=g^{\prime }(1)=m$ $\Rightarrow$ $m=2a+b$ $(3)$ $f^{\prime }(6)=h^{\prime }(6)=2$ $\Rightarrow$ $2=12a+b$ $(4)$

Somit erhält man vier Gleichungen für $4$ Unbekannte $a,b,c,m$.

Das GLS kann z.B. mit einem Taschenrechner, der Gleichungssysteme mit $4$

Unbekannten verarbeiten kann, gelöst werden, z.B. der Casio fx-991DE X.

Hier wird das Additionsverfahren verwendet.

Gleichung $(4)$$\cdot (-5)$ $\Rightarrow$ $-10=-60a-5b$

$(2)-(1)\Rightarrow$ $3=35a+5b$

Addiert man beide Gleichungen erhält man: $-7=-25a$ $\Rightarrow$ $a={\displaystyle \frac{7}{25}}$

Setzt man $a$ in Gleichung $(4)$ ein $\Rightarrow$ $2=12\cdot {\displaystyle \frac{7}{25}}+b\Rightarrow b=-{\displaystyle \frac{34}{25}}$

Aus Gleichung $(1)\Rightarrow c=2-a-b=2-{\displaystyle \frac{7}{25}}-(-{\displaystyle \frac{34}{25}})={\displaystyle \frac{77}{25}}$

Aus Gleichung $(3)\Rightarrow m=2\cdot {\displaystyle \frac{7}{25}}-{\displaystyle \frac{34}{25}}=-{\displaystyle \frac{20}{25}}=-{\displaystyle \frac{4}{5}}$

Mit dem Punkt $A(1|2)$ und $g(x)=mx+n$ folgt:

$2=m\cdot 1+n\Rightarrow n=2-m=2-(-{\displaystyle \frac{4}{5}})={\displaystyle \frac{14}{5}}$

Antwort: Die gesuchten Funktionen haben die Gleichungen $g(x)=-{\displaystyle \frac{4}{5}}x+{\displaystyle \frac{14}{5}}$

bzw. $g(x)=-\mathrm{0,8}x+\mathrm{2,8}$ und $f(x)={\displaystyle \frac{7}{25}}{x}^2-{\displaystyle \frac{34}{25}}x+{\displaystyle \frac{77}{25}}$

Ein „krümmungsruckfreier“ Übergang an einer Stelle $x_0$ bzw. $x_1$ ist möglich, wenn die Bedingungen $f^{\prime \prime }(x_0)=g^{\prime \prime }(x_0)$ bzw. $f^{\prime \prime }(x_1)=h^{\prime \prime }(x_1)$erfüllt sind.

Im Punkt $A(1|2)$ gilt:

$g(x)=-\mathrm{0,8}x+\mathrm{2,8}$

$g^{\prime }(x)=-\mathrm{0,8}$

$g^{\prime \prime }(x)=0;g^{\prime \prime }(1)=0$

$f(x)={\displaystyle \frac{7}{25}}{x}^2-{\displaystyle \frac{34}{25}}x+{\displaystyle \frac{77}{25}}$

$f^{\prime }(x)={\displaystyle \frac{14}{25}}x-{\displaystyle \frac{34}{25}}$

$f^{\prime \prime }(x)={\displaystyle \frac{14}{25}};f^{\prime \prime }(1)={\displaystyle \frac{14}{25}}\Rightarrow$   ${\displaystyle \frac{14}{25}}\ne 0$    

also findet im Punkt $A$ ein Krümmungsruck statt.

Analog gilt für den Punkt $B(6|5)$:

$h(x)=2x-7$

$h^{\prime }(x)=2$

$h^{\prime \prime }(x)=0;h^{\prime \prime }(6)=0$

$f^{\prime \prime }(6)={\displaystyle \frac{14}{25}}\Rightarrow$${\displaystyle \frac{14}{25}}\ne 0$

also findet auch im Punkt $B$ ein Krümmungsruck statt.

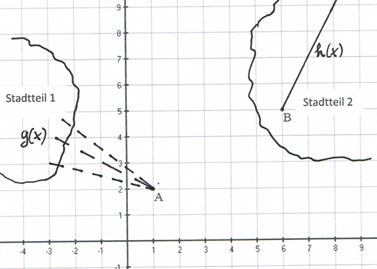
Gegeben sind die beiden Funktionen $g(x)=-\mathrm{0,8}x+\mathrm{2,8}$ und $h(x)=2x-7$

sowie die beiden Punkte $A(1|2)$ und $B(6|5)$.

$g^{\prime }(x)=-\mathrm{0,8}$

$g^{\prime \prime }(x)=0;g^{\prime \prime }(1)=0$

$h^{\prime }(x)=2$

$h^{\prime \prime }(x)=0;h^{\prime \prime }(6)=0$

Ansatz für die Funktion $k(x)$: $k(x)=a{x}^4+b{x}^3+c{x}^2+dx+e$

Die erste Ableitung von $k(x)$ lautet: $k^{\prime }(x)=4a{x}^3+3b{x}^2+2cx+d$

Die zweite Ableitung von $k(x)$ lautet: $k^{\prime \prime }(x)=12a{x}^2+6bx+2c$

Damit ergeben sich die folgenden Gleichungen:

1. versatzfrei:  $k(1)=g(1)=2$ $\Rightarrow$   $2=a+b+c+d+e$                   $(1)$                  $k(6)=h(6)=5$  $\Rightarrow$     $5=1296a+216b+36c+6d+e$     $(2)$2.knickfrei:     $k^{\prime }(1)=g^{\prime }(1)=-\mathrm{0,8}$ $\Rightarrow$   $-\mathrm{0,8}=4a+3b+2c+d$      $(3)$

  $k^{\prime }(6)=h^{\prime }(6)=2$ $\Rightarrow$     $2=864a+108b+12c+d$ $(4)$

3.ruckfrei: $k^{\prime \prime }(1)=g^{\prime \prime }(1)=0$$$ $\Rightarrow$ $0=12a+6b+2c$ $(5)$

  $k^{\prime \prime }(6)=h^{\prime \prime }(6)=0$ $\Rightarrow$ $0=432a+36b+2c$ $(6)$

Somit erhält man sechs Gleichungen für 5 Unbekannte.

Aus diesen 6 Gleichungen wähle ich die Gleichungen $(1),(3),(4),(5)$ und $(6)$ aus.

Zur Vereinfachung der Rechnung werden Zeilen und Spalten vertauscht.

Dadurch ändert sich Reihenfolge der Variablen und man erhält das folgende Gleichungssystem:

$e+d+c+b+a=2$

$d+2c+3b+4a=-\mathrm{0,8}$

$d+12c+108b+864a=2$

$2c+6b+12a=0$

$2c+36b+432a=0$

Die erweiterte Koeffizientenmatrix lautet:

$\left(\begin{array}{rrrrrc}1& 1& 1& 1& 1& 2\\ 0& 1& 2& 3& 4& -\mathrm{0,8}\\ 0& 1& 12& 108& 864& 2\\ 0& 0& 2& 6& 12& 0\\ 0& 0& 2& 36& 432& 0\end{array}\right)$

Die Koeffizientenmatrix wird durch geeignete Umformungen so bearbeitet, dass unterhalb der Diagonalen nur Nullen stehen.

$\left(\begin{array}{rrrrrc}1& 1& 1& 1& 1& 2\\ 0& 1& 2& 3& 4& -\mathrm{0,8}\\ 0& 1& 12& 108& 864& 2\\ 0& 0& 2& 6& 12& 0\\ 0& 0& 2& 36& 432& 0\end{array}\right)\underrightarrow{\mathrm{III}-\mathrm{II}}$

$\left(\begin{array}{rrrrrc}1& 1& 1& 1& 1& 2\\ 0& 1& 2& 3& 4& -\mathrm{0,8}\\ 0& 0& 10& 105& 860& \mathrm{2,8}\\ 0& 0& 2& 6& 12& 0\\ 0& 0& 2& 36& 432& 0\end{array}\right)\underrightarrow{\mathrm{IV}\cdot (-5)+\mathrm{III}}$

$\left(\begin{array}{rrrrrc}1& 1& 1& 1& 1& 2\\ 0& 1& 2& 3& 4& -\mathrm{0,8}\\ 0& 0& 10& 105& 860& \mathrm{2,8}\\ 0& 0& 0& 75& 800& \mathrm{2,8}\\ 0& 0& 2& 36& 432& 0\end{array}\right)\underrightarrow{\mathrm{V}\cdot (-5)+\mathrm{III}}$

$\left(\begin{array}{rrrrrc}1& 1& 1& 1& 1& 2\\ 0& 1& 2& 3& 4& -\mathrm{0,8}\\ 0& 0& 10& 105& 860& \mathrm{2,8}\\ 0& 0& 0& 75& 800& \mathrm{2,8}\\ 0& 0& 0& -75& -1300& \mathrm{2,8}\end{array}\right)\underrightarrow{\mathrm{V}+\mathrm{IV}}$

$\left(\begin{array}{rrrrrc}1& 1& 1& 1& 1& 2\\ 0& 1& 2& 3& 4& -\mathrm{0,8}\\ 0& 0& 10& 105& 860& \mathrm{2,8}\\ 0& 0& 0& 75& 800& \mathrm{2,8}\\ 0& 0& 0& 0& -500& \mathrm{5,6}\end{array}\right)$

Beachte die Reihenfolge der Variablen. An der fünften Stelle steht die Variable $a$ .

Somit folgt aus der letzten Zeile der umgewandelten Koeffizientenmatrix :

$-500a=\mathrm{5,6}\Rightarrow a=-{\displaystyle \frac{7}{625}}$

Aus Gleichung $IV$ folgt: $75b+800\cdot (-{\displaystyle \frac{7}{625}})=\mathrm{2,8}\Rightarrow b={\displaystyle \frac{98}{625}}$

Aus Gleichung $III$ folgt: $10c+105\cdot ({\displaystyle \frac{98}{625}})+860\cdot (-{\displaystyle \frac{7}{625}})=\mathrm{2,8}\Rightarrow c=-{\displaystyle \frac{252}{625}}$

Aus Gleichung $II$ folgt: $d+2\cdot (-{\displaystyle \frac{252}{625}})+3\cdot ({\displaystyle \frac{98}{625}})+4\cdot (-{\displaystyle \frac{7}{625}})=-\mathrm{0,8}\Rightarrow d=-{\displaystyle \frac{262}{625}}$

Aus Gleichung $I$ folgt: $e+(-{\displaystyle \frac{262}{625}})+(-{\displaystyle \frac{252}{625}})+({\displaystyle \frac{98}{625}})+(-{\displaystyle \frac{7}{625}})=2\Rightarrow$

$e={\displaystyle \frac{1673}{625}}$

Die berechneten Werte für die Variablen $a,b,c,d$ und $e$ müssen noch in die nicht verwendete Gleichung $(2)$ eingesetzt werden.

$5=1296\cdot (-{\displaystyle \frac{7}{625}})+216\cdot ({\displaystyle \frac{98}{625}})+36\cdot (-{\displaystyle \frac{252}{625}})+6\cdot (-{\displaystyle \frac{262}{625}})+{\displaystyle \frac{1673}{625}}={\displaystyle \frac{3125}{625}}=5$

Somit hat man eine wahre Aussage erhalten und das Gleichungssystem ist lösbar.

Anmerkung: Die Gleichungen $(3),(4),(5)$ und $(6)$ können auch mit einem TR gelöst werden. Mit dem Ergebnis kann aus Gleichung $(1)$ $e$ berechnet werden und anschließend überprüft man noch Gleichung $(2)$.

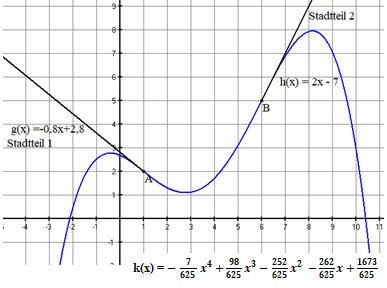
Antwort: Die gesuchte Funktion $k(x)$ lautet:

$k(x)$ =   $(-{\displaystyle \frac{7}{625}})x^4+({\displaystyle \frac{98}{625}})x^3-({\displaystyle \frac{252}{625}})x^2-{\displaystyle \frac{262}{625}}x+{\displaystyle \frac{1673}{625}}$

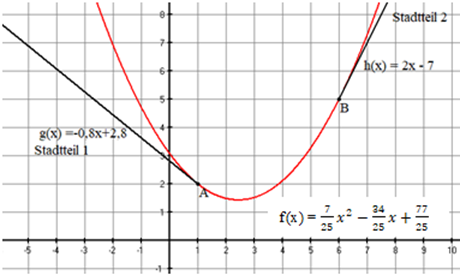
In der Aufgabenstellung nicht gefordert ist eine Zeichnung mit den Funktionen $g(x),h(x)$ und $k(x)$.

So würde das Ergebnis aussehen.



Die Verbindung der Punkte $A$ und $B$ erfolgt nicht nur knickfrei sondern auch ruckfrei. An den Verbindungsstellen $A$ und $B$ befindet sich jeweils ein Wendepunkt der Funktion $k(x)$.