Analysis, Teil B, Aufgabengruppe 2
Gegeben ist die Funktion mit und . Abbildung 1 zeigt den Graphen von sowie die einzige Nullstelle von .
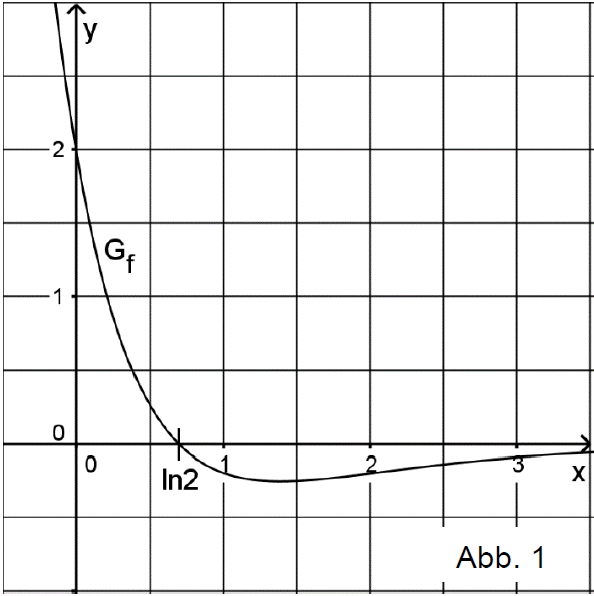
Zeigen Sie, dass für den Term der Ableitungsfunktion von gilt: . (3 BE)
Bestimmen Sie rechnerisch Lage und Art des Extrempunkts von . (4 BE)
(Teilergebnis: x-Koordinate des Extrempunkts: )
Zusätzlich ist die Funktion mit und gegeben.
Zeigen Sie, dass eine Stammfunktion von ist, und begründen Sie anhand des Terms von , dass gilt. (3 BE)
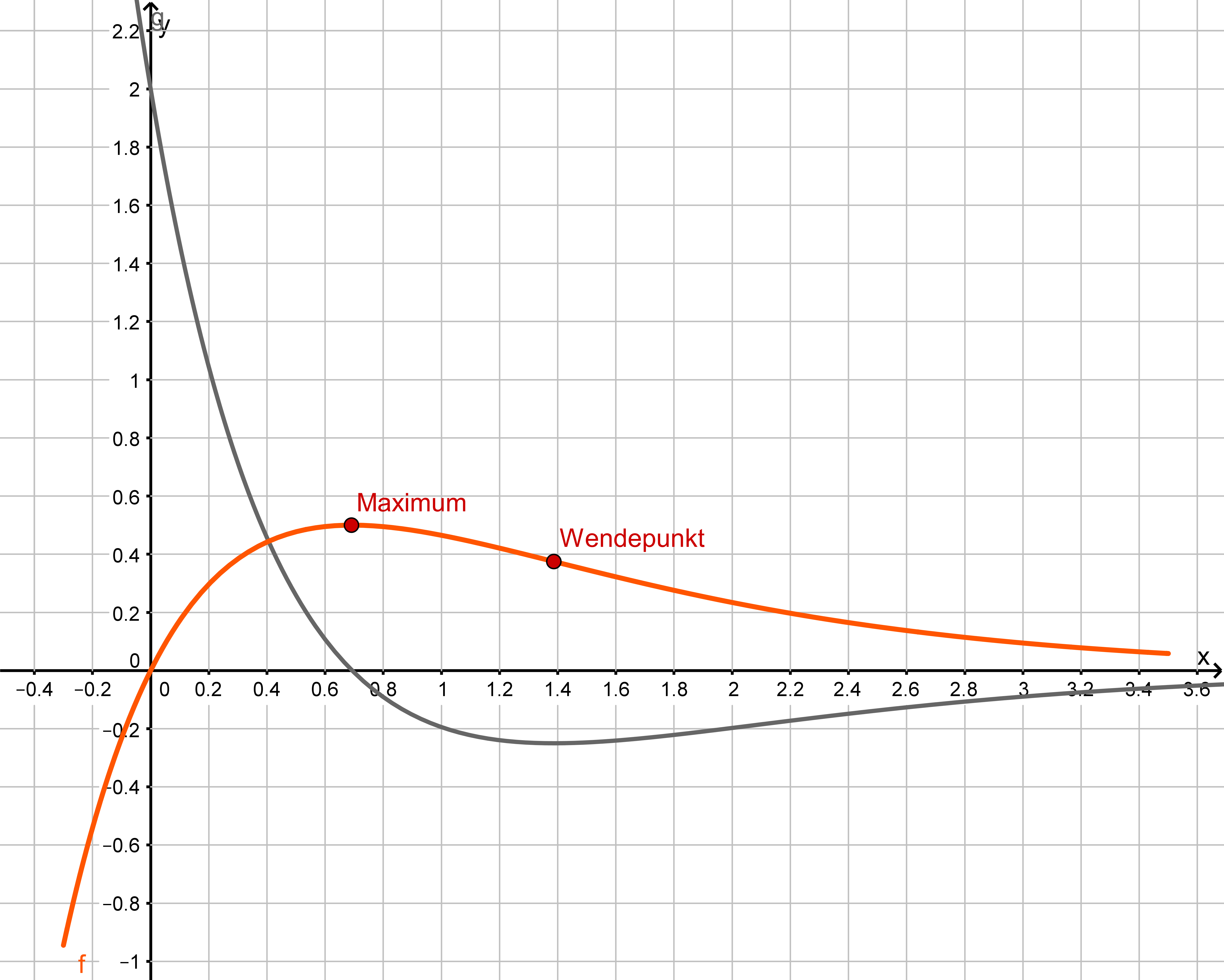
Der Graph von verläuft durch den Punkt . Begründen Sie ohne weitere Rechnung, dass keine größeren Werte als annehmen kann und bei eine Wendestelle besitzt. Berechnen Sie die y-Koordinate des zugehörigen Wendepunkts. (5 BE)
Zeichnen Sie den Graphen von unter Berücksichtigung der bisherigen Ergebnisse sowie des Funktionswerts im Bereich in Abbildung 1 ein. (4 BE)
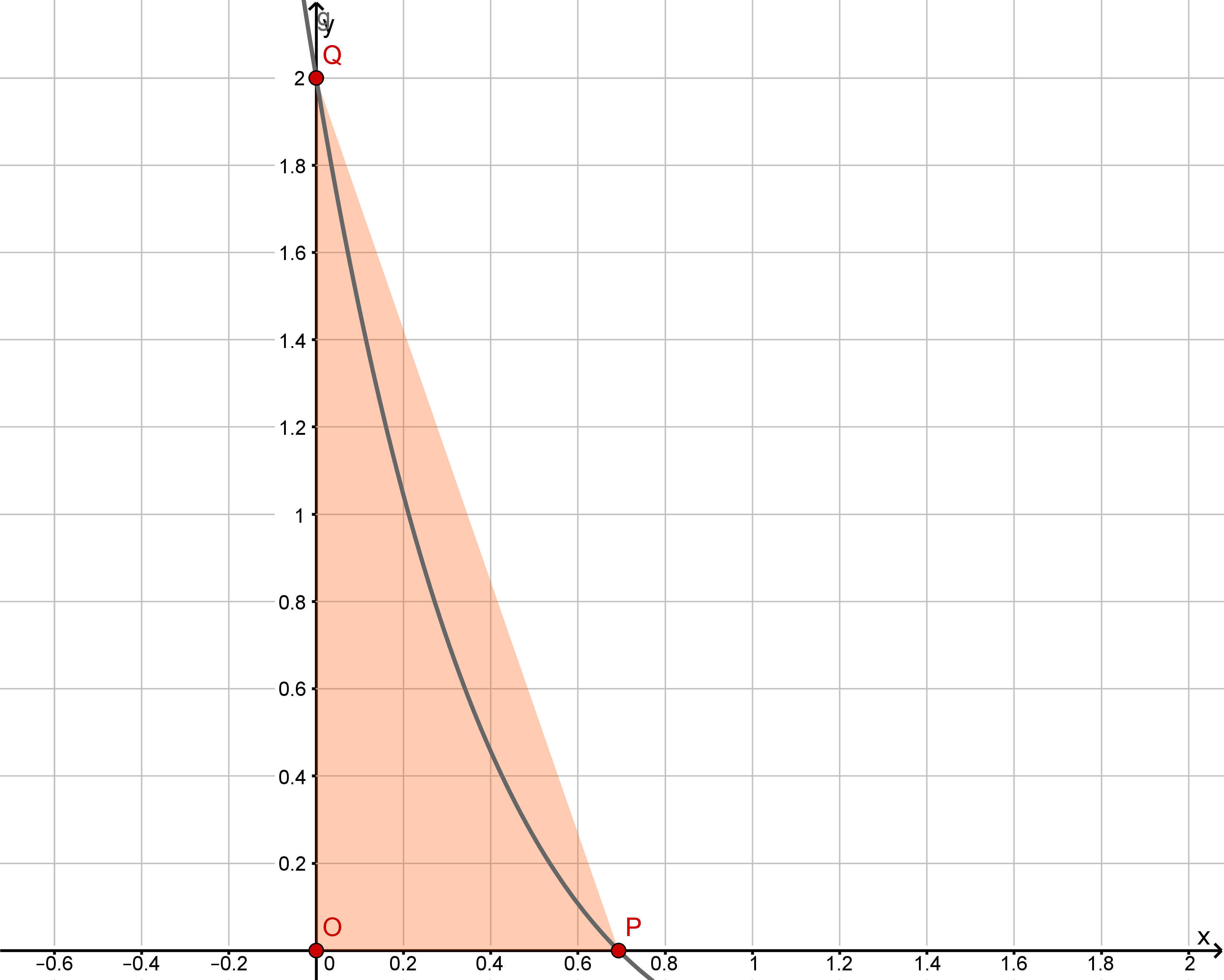
Der Graph von schließt mit den Koordinatenachsen ein Flächenstück ein, das durch das Dreieck mit Eckpunkten , und angenähert werden kann. Berechnen Sie, um wie viel Prozent der Flächeninhalt des Dreiecks vom Inhalt des Flächenstücks abweicht. (4 BE)
Betrachtet wird nun die Integralfunktion mit und .
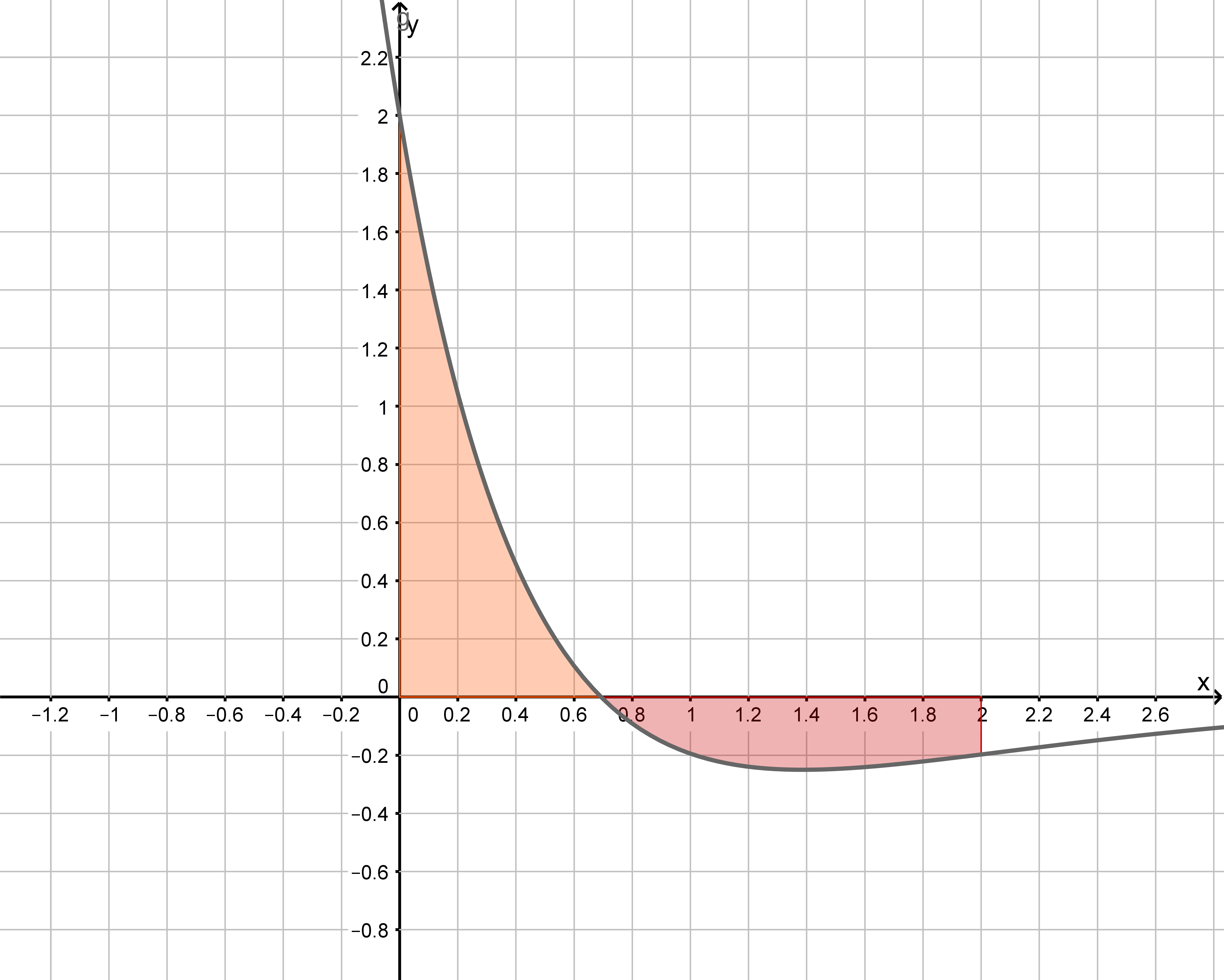
Begründen Sie, dass mit der betrachteten Stammfunktion von übereinstimmt. Interpretieren Sie geometrisch den Wert mithilfe von in Abbildung 1 geeignet zu markierenden Flächenstücken. (4 BE)
Geben Sie den Term einer in definierten Funktion an, die eine Stammfunktion, aber keine Integralfunktion von ist. (2 BE)
Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das? serlo.org