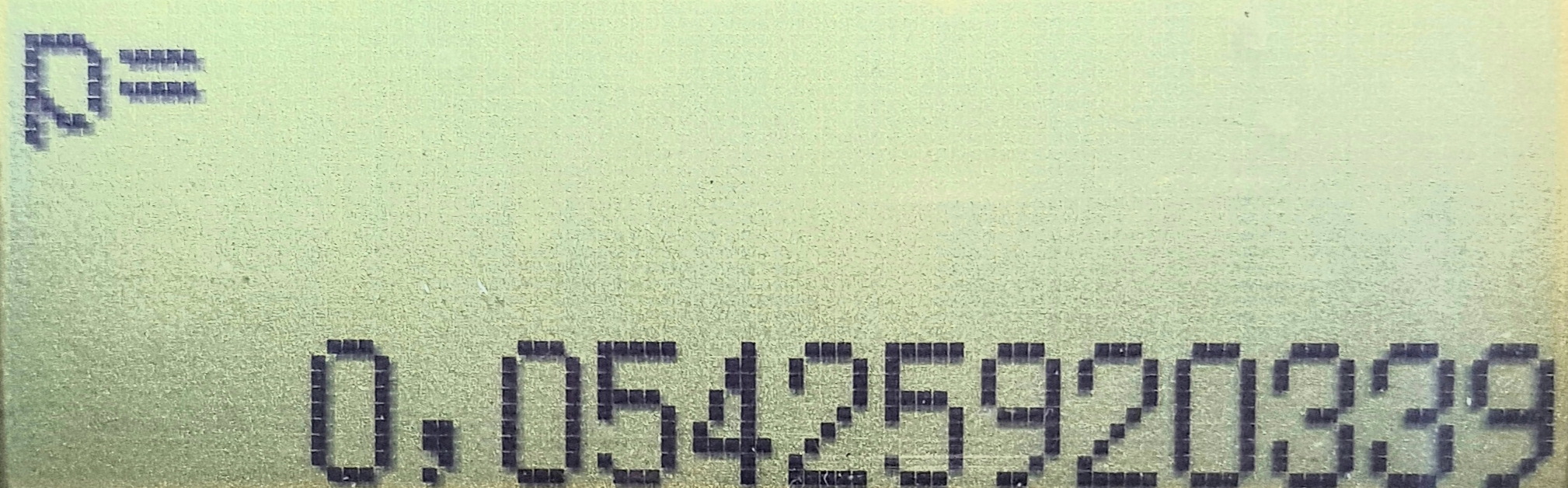Aufgaben

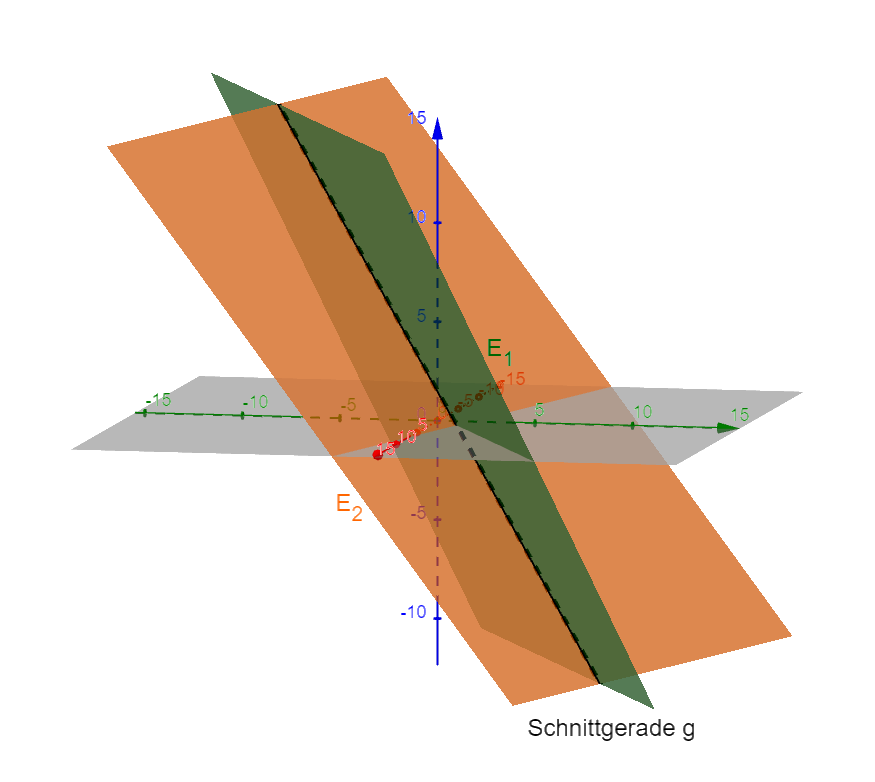
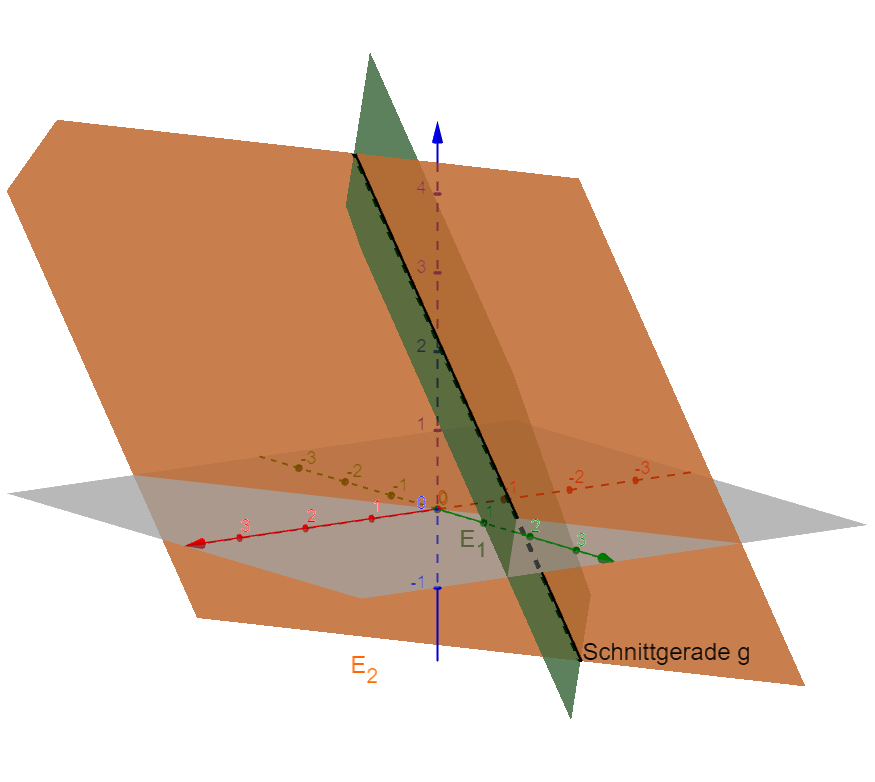
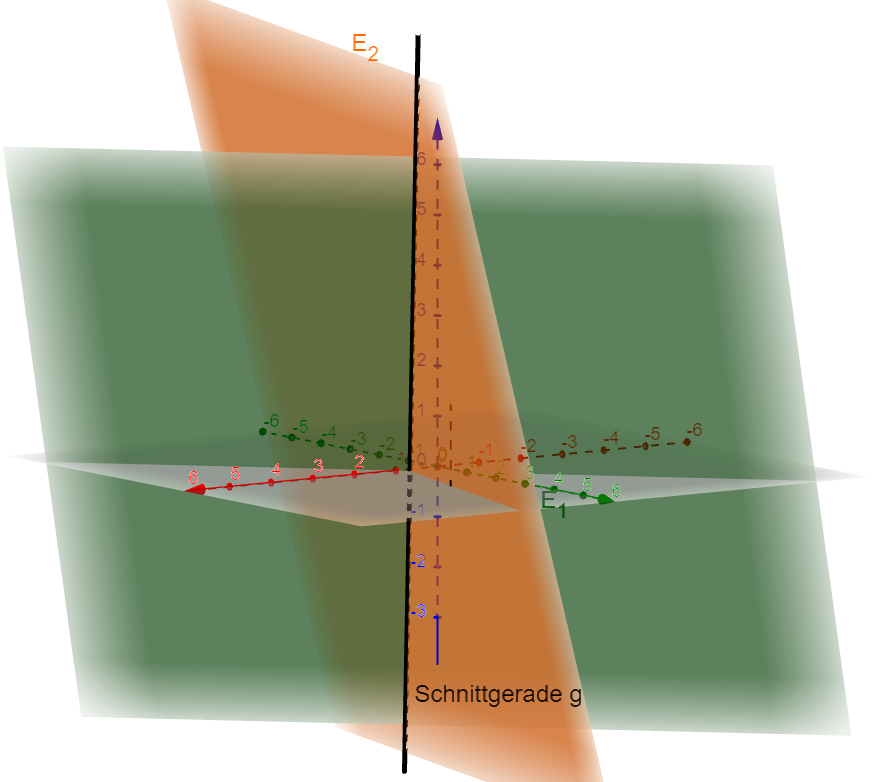
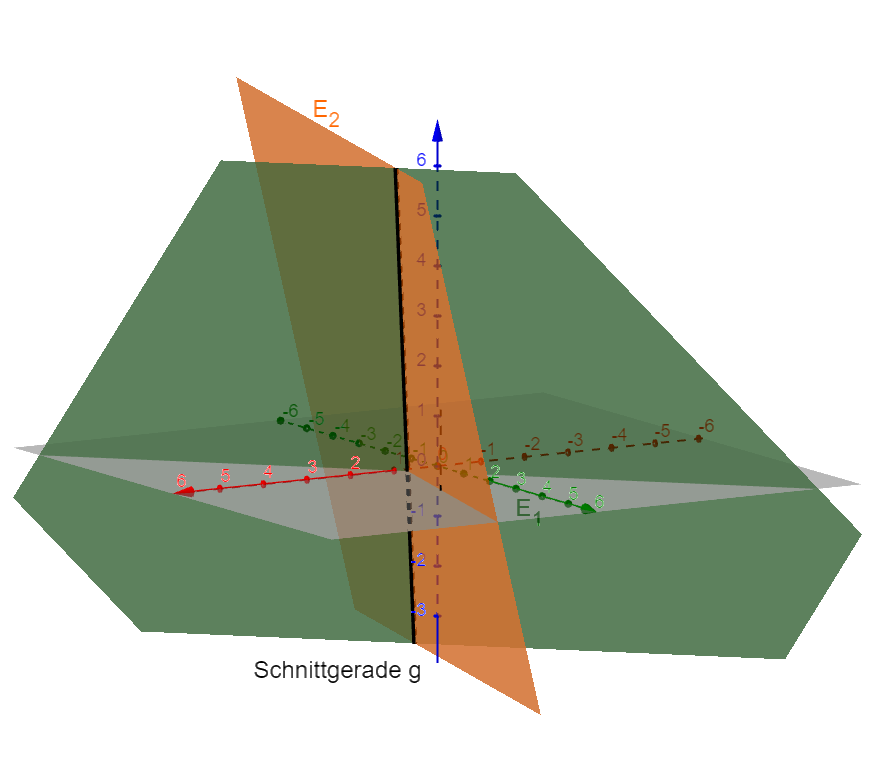
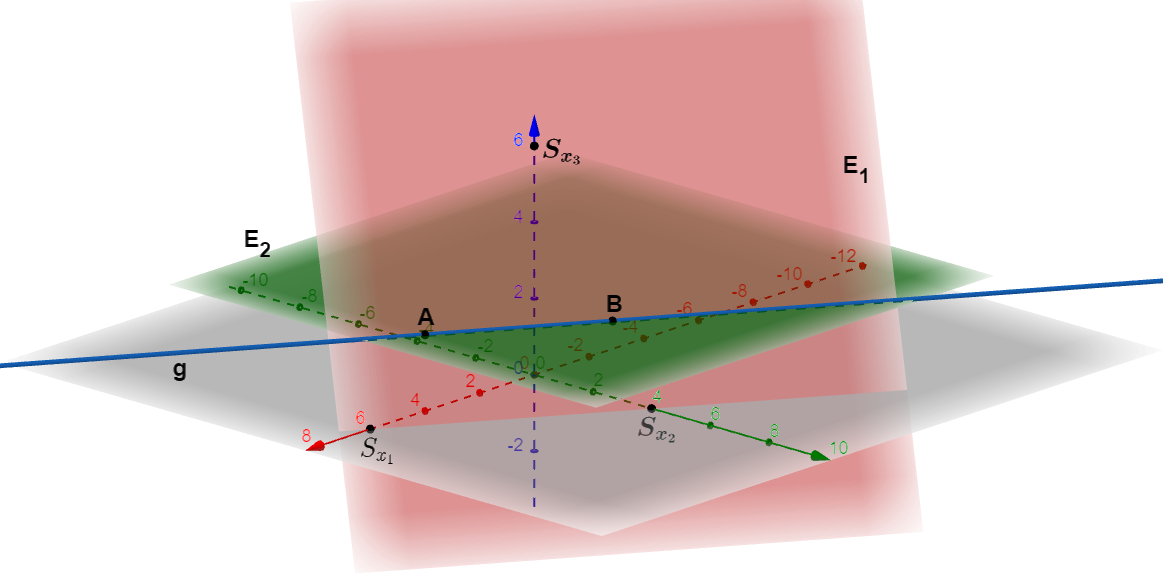
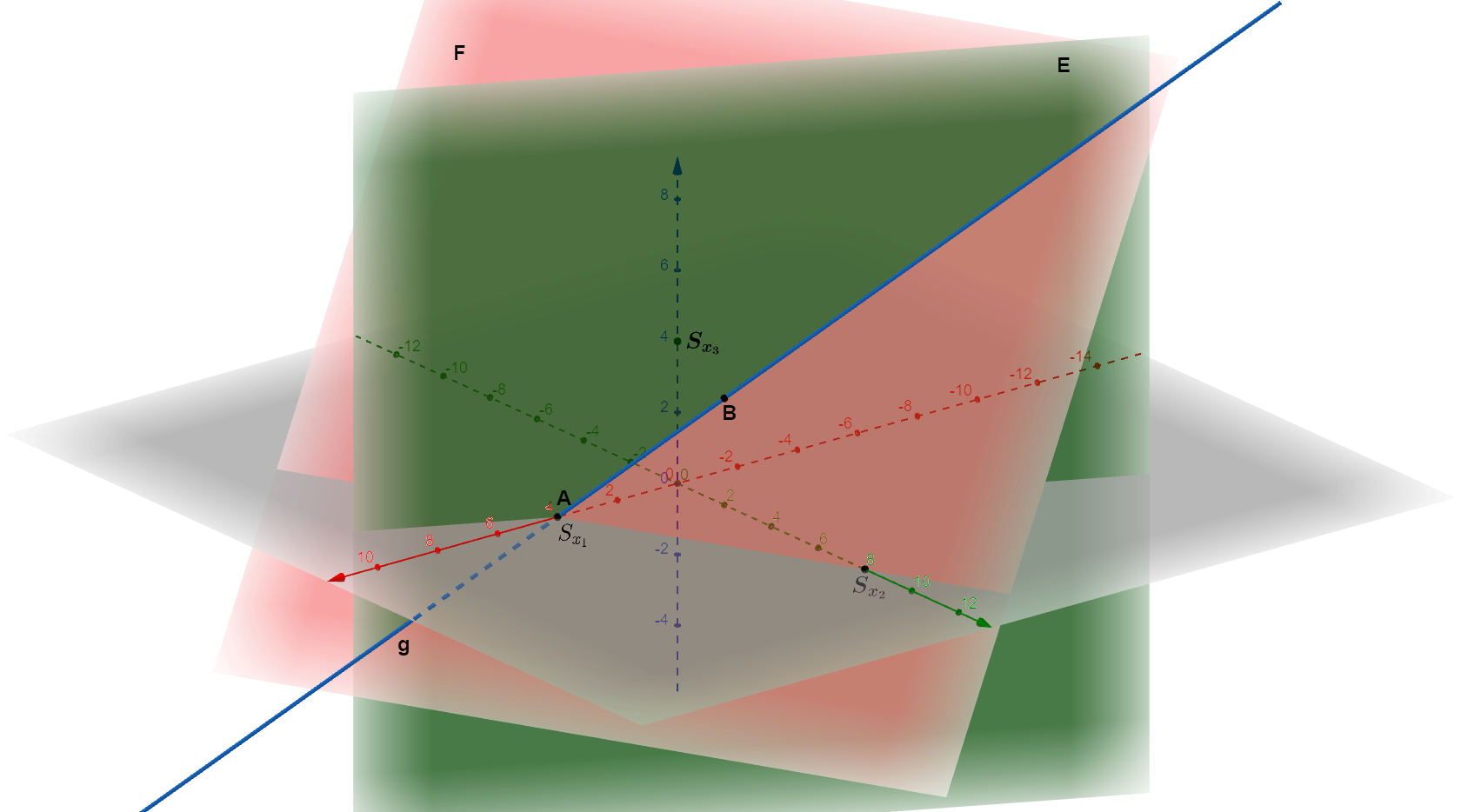
Gegenseitige Lage von Geraden und Ebenen

Wenn man eine Gerade und eine Ebene betrachtet, gibt es 3 verschiedene Möglichkeiten der gegenseitigen

Lage zueinander.

1. Die Gerade schneidet die Ebene in einem Punkt.

2. Die Gerade ist echt parallel zur Ebene.

3. Die Gerade liegt in der Ebene.

Vorgehensweise bei der Lagebestimmung

1. Um die Lagebeziehung zwischen einer Geraden und einer Ebene zu bestimmen, ist es empfehlenswert wenn man eine Parametergleichung der Geraden und eine Koordinatengleichung der Ebene verwendet.

2. Die Geradengleichung wird in die Koordinatenform der Ebene eingesetzt.

3. Die Gleichung wird nach der Variablen aufgelöst. Dabei sind verschiedene Ergebnisse möglich, die einen Rückschluss auf die Lagebeziehung zwischen Gerade und Ebene erlauben.

Mögliche Ergebnisse, die bei der Gleichungsauflösung auftreten können:

Ergebnis	Beispiel für Lösung	Lagebeziehung
genau eine Lösung	$r = 1$ oder $r = - 3$	Die Gerade schneidet die Ebene in einem Punkt S. Den Schnittpunkt erhält man durch Einsetzen des errechneten Wertes von r in die Geradengleichung.
keine Lösung	$3 = 5$ oder $8 = 0$	Die Gerade und die Ebene sind echt parallel und haben keinen gemeinsamen Punkt.
unendlich viele Lösungen	$1 = 1$ oder $0 = 0$	Die Gerade liegt in der Ebene und alle Punkte auf der Geraden liegen in der Ebene.

Um zu verdeutlichen, wie das Ganze genau funktionieren soll, folgt hier zu jeder Möglichkeit jeweils ein Beispiel zum Ausklappen.

Im Spoiler findet man Lösungen für andere Formen der Ebenengleichung.

2
Axialschnitt eines Rotationskörpers
Schneidet man einen Rotationskörper längs seiner Achse durch, erhält man den Axialschnitt des Körpers.
Die folgende Tabelle zeigt die Zuordnung zwischen einem Rotationskörper und dem dazugehörenden Axialschnitt.
Rotationskörper
Axialschnitt
Zylinder
Rechteck
Kegel
gleichschenkliges Dreieck
Kugel
Kreis
Halbkugel
Halbkreis
Kegelstumpf
gleichschenkliges Trapez
Wenn du lernen willst wie man einen Rotationskörper auf das Papier zeichnet, gehe auf den Artikel Skizzieren eines Rotationskörpers - Anleitung.
3
Für jedes $a \in ℝ \ {0}$ ist die Funktionenschar gegeben durch $f_{a} (x) = x \cdot e^{a x} + \frac{3}{a}$ .
Der Graph der Funktion ist $K_{a}$ .
Gib bei allen Teilaufgaben die Ergebnisse in Abhängigkeit vom Scharparameter $a$ an.
1. Wo schneiden die Scharkurven die $y$ -Achse?
2. Untersuche $K_{a}$ auf Hoch- und Tiefpunkte.
3. Bestimme das Verhalten der Funktion $f_{a} (x)$ für $x \to - \infty$ und für $x \to \infty$ und gib gegebenenfalls die Asymptote an.
4. Skizziere für $a = - 3$ und $a = 1$ die Graphen von $K_{- 3}$ und von $K_{1}$ .
5. Welche Scharkurve hat für $x = \frac{1}{2}$ ein Extremum?
6. Auf welcher Ortskurve liegen die Extrema?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
Lösung zu 1
Die $y$ -Achse wird für $x = 0$ geschnitten.
Setze $x = 0$ in die Funktionsgleichung ein:
$f_{a} (0) = 0 \cdot e^{a \cdot 0} + \frac{3}{a} = 0 \cdot 1 + \frac{3}{a} = \frac{3}{a}$
Antwort: Der Schnittpunkt der Scharkurven mit der $y$ -Achse hat die Koordinaten $S_{y} (0 | \frac{3}{a})$ .
Lösung zu 2
Die notwendige Bedingung für ein Extremum lautet: $f_{a}^{'} (x) = 0$
Berechne die 1. Ableitung, beachte dabei die Produktregel und die Kettenregel:
$f_{a}^{'} (x) = 1 \cdot e^{a x} + x \cdot e^{a x} \cdot a = (1 + a \cdot x) \cdot e^{a x}$
Setze $f_{a}^{'} (x) = 0$
$\Rightarrow 0 = \underset{= 0}{\underset{⏟}{(1 + a \cdot x)}} \cdot \underset{immer > 0}{\underset{⏟}{e^{a \cdot x}}}$
Nur die Klammer kann null werden:
$0 = 1 + a \cdot x \Rightarrow x = - \frac{1}{a}$
Die Feststellung, ob sich an der Stelle $x = - \frac{1}{a}$ ein Extremum befindet, kann mit einer Monotonietabelle oder der 2. Ableitung erfolgen. Hier erfolgt die Überprüfung mit der 2. Ableitung:
Ist $f_{a}^{''} (x) > 0$ , dann hat die Scharkurve $K_{a}$ an der Stelle $x$ einen Tiefpunkt.
Ist $f_{a}^{''} (x) < 0$ , dann hat die Scharkurve $K_{a}$ an der Stelle $x$ einen Hochpunkt.
Berechne die 2. Ableitung, beachte dabei wieder die Produktregel und die Kettenregel:
$f_{a}^{'} (x) = (1 + a \cdot x) \cdot e^{a x}$
$f_{a}^{''} (x) = a \cdot e^{a x} + (1 + a \cdot x) \cdot e^{a x} \cdot a = (a^{2} \cdot x + 2 a) \cdot e^{a x}$
Setze $x = - \frac{1}{a}$ in $f_{a}^{''} (x) = (a^{2} \cdot x + 2 a) \cdot e^{a x}$ ein:
$f_{a}^{''} (- \frac{1}{a}) = (a^{2} \cdot (- \frac{1}{a}) + 2 a) \cdot e^{a \cdot (- \frac{1}{a})} = (- a + 2 a) \cdot e^{- 1} = a \cdot e^{- 1}$
Das Ergebnis ist vom Scharparameter $a$ abhängig, d.h. es ist eine Fallunterscheidung bzgl. des Vorzeichens von $a$ erforderlich.
Fallunterscheidung
Fall 1: $a > 0$
$f_{a}^{''} (- \frac{1}{a}) = a \cdot e^{- 1} > 0 \Rightarrow TP$
Fall 2: $a < 0$
$f_{a}^{''} (- \frac{1}{a}) = a \cdot e^{- 1} < 0 \Rightarrow HP$
Setze $x = - \frac{1}{a}$ in $f_{a} (x)$ ein, um die $y$ -Koordinate der Extrema zu berechnen.
$f_{a} (- \frac{1}{a}) = (- \frac{1}{a}) \cdot e^{a \cdot (- \frac{1}{a})} + \frac{3}{a} = \frac{3}{a} - \frac{1}{a} \cdot e^{- 1} = \frac{1}{a} \cdot (3 - e^{- 1})$
Antwort: Für $a > 0$ hat der Tiefpunkt die Koordinaten $T P (- \frac{1}{a} | \frac{1}{a} \cdot (3 - e^{- 1}))$ und für $a < 0$ hat der Hochpunkt die Koordinaten $H P (- \frac{1}{a} | \frac{1}{a} \cdot (3 - e^{- 1}))$ .
Lösung zu 3
Betrachte zunächst $\lim_{x \to + \infty} (x \cdot e^{a x} + \frac{3}{a})$ . Wie verhält sich der Ausdruck $x \cdot e^{a x}$ , wenn $x$ sehr groß wird? Das Verhalten hängt vom Vorzeichen des Scharparameters $a$ ab, d.h. es ist eine Fallunterscheidung bzgl. des Vorzeichens von $a$ erforderlich.
Fallunterscheidung
Fall 1: $a > 0$
$\lim_{x \to + \infty} (x \cdot e^{a x} + \frac{3}{a}) = \lim_{x \to + \infty} \underset{\to + \infty}{\underset{⏟}{x \cdot e^{a x}}} + \frac{3}{a} = + \infty$
Für $a > 0$ wächst $e^{a x}$ für $x \to + \infty$ stärker als jede Potenz von $x$ . Der Ausdruck $x \cdot e^{a x}$ geht somit gegen $+ \infty$ .
$\lim_{x \to - \infty} (x \cdot e^{a x} + \frac{3}{a}) = \lim_{x \to - \infty} \underset{\to 0}{\underset{⏟}{x \cdot e^{a x}}} + \frac{3}{a} = \frac{3}{a}$
Für $a > 0$ geht $e^{a x}$ für $x \to - \infty$ stärker gegen $0$ als $x \to - \infty$ . Der Ausdruck $x \cdot e^{a x}$ geht somit gegen $0$ .
Fall 2: $a < 0$
$\lim_{x \to + \infty} (x \cdot e^{a x} + \frac{3}{a}) = \lim_{x \to + \infty} \underset{\to 0}{\underset{⏟}{x \cdot e^{a x}}} + \frac{3}{a} = \frac{3}{a}$
Für $a < 0$ geht $e^{a x}$ für $x \to + \infty$ stärker gegen $0$ als $x \to + \infty$ . Der Ausdruck $x \cdot e^{a x}$ geht somit gegen $0$ .
$\lim_{x \to - \infty} (x \cdot e^{a x} + \frac{3}{a}) = \lim_{x \to - \infty} \underset{\to - \infty}{\underset{⏟}{x \cdot e^{a x}}} + \frac{3}{a} = - \infty$
Für $a < 0$ wächst $e^{a x}$ für $x \to - \infty$ stärker als jede Potenz von $x$ . Der Ausdruck $x \cdot e^{a x}$ geht somit gegen $- \infty$ .
Alle Scharkurven haben eine waagrechte Asymptote $y_{A} = \frac{3}{a}$ .
Lösung zu 4
Für $a = - 3$ lautet $f_{- 3} (x) = x \cdot e^{- 3 x} - 1$ und für $a = 1$ ist $f_{1} = x \cdot e^{x} + 3$ . Bekannt sind weiterhin der Schnittpunkt mit der y-Achse $S_{y} (0 | \frac{3}{a})$ , der Extrempunkt $E (- \frac{1}{a} | \frac{1}{a} \cdot (3 - e^{- 1}))$ und die waagrechte Asymptote $y_{A} = \frac{3}{a}$ . Zum Skizzieren der beiden Graphen ist es sinnvoll, noch einige Funktionswerte zu berechnen. Sie sind in den beiden folgenden Tabellen aufgelistet.
Tabelle für $f_{- 3} (x) = x \cdot e^{- 3 x} - 1$ :
x
$f_{- 3} (x)$
besonderer Punkt
-0,5
-3,24
0
-1
$S_{y}$
0,33
-0,88
HP
1
-0,95
3
-1
Die Funktion $f_{- 3} (x) = x \cdot e^{- 3 x} - 1$ hat die waagrechte Asymptote $y_{A} = - 1$ .
Tabelle für $f_{1} = x \cdot e^{x} + 3$ :
x
$f_{1} (x)$
besonderer Punkt
-3
2,85
-2
2,73
-1
2,63
TP
0
3
$S_{y}$
0,5
3,82
1
5,72
Die Funktion $f_{1} (x) = x \cdot e^{x} + 3$ hat die waagrechte Asymptote $y_{A} = 3$ .
Darstellung der Graphen von $K_{- 3}$ und von $K_{1}$ .
Lösung zu 5
Ein Extremum liegt vor, wenn $f_{a}^{'} (x) = 0$ ist.
Setze in die unter Lösung $2$ berechnete Ableitung $f_{a}^{'} (x) = (1 + a \cdot x) \cdot e^{a x}$ den Wert $x = \frac{1}{2}$ ein:
$f_{a}^{'} (\frac{1}{2}) = e^{a \cdot \frac{1}{2}} \cdot (1 + a \cdot \frac{1}{2})$
Setze $f_{a}^{'} (\frac{1}{2}) = 0$
$\Rightarrow 0 = \underset{immer > 0}{\underset{⏟}{e^{a \cdot \frac{1}{2}}}} \cdot \underset{= 0}{\underset{⏟}{(1 + a \cdot \frac{1}{2})}}$
Nur die Klammer kann null werden:
$0 = 1 + a \cdot \frac{1}{2} \Rightarrow a = - 2$
Antwort: Für $a = - 2$ hat die Scharfunktion $f_{- 2} (x) = x \cdot e^{- 2 x} - \frac{3}{2}$ an der Stelle $x = \frac{1}{2}$ ein Extremum.
Lösung zu 6
Für die Ortskurve der Extrema benötigst du die Extrempunktkoordinaten.
Das Extremum hat die Koordinaten $E (- \frac{1}{a} | \frac{1}{a} \cdot (3 - e^{- 1}))$ .
Für die Berechnung der Ortskurve setzt du $x = - \frac{1}{a}$ und $y = \frac{1}{a} \cdot (3 - e^{- 1})$ .
Löse dann $x = - \frac{1}{a}$ nach $a$ auf $\Rightarrow a = - \frac{1}{x}$ .
Setze $a = - \frac{1}{x}$ in $y = \frac{1}{a} \cdot (3 - e^{- 1})$ ein:
$y = \frac{1}{- \frac{1}{x}} \cdot (3 - e^{- 1}) = - x \cdot (3 - e^{- 1}) = (e^{- 1} - 3) \cdot x$
Antwort: Die Gleichung der Ortskurve lautet $y = (e^{- 1} - 3) \cdot x$ . Der Graph der Ortskurve ist eine Ursprungsgerade mit der Steigung $m = e^{- 1} - 3 \approx - 2,63$ .
Zur Veranschaulichung sind im folgenden Applet mehrere Scharkurven und die Ortskurve der Extrema dargestellt.
Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unsererDatenschutzerklärung.
4
Gegeben sind die beiden windschiefen Geraden $g : \vec{O X} = (\begin{array}{c} 5 \\ 0 \\ 1 \end{array}) + r \cdot (\begin{array}{c} - 4 \\ 1 \\ 1 \end{array})$ und
$h : \vec{O X} = (\begin{array}{c} 5 \\ 3 \\ 7 \end{array}) + s \cdot (\begin{array}{c} 2 \\ 1 \\ - 2 \end{array})$
Berechne ihren Abstand und die beiden Lotfußpunkte auf den Geraden.
Hinweis: Verwende bei der Lösung dieser Aufgabe die Differentialrechnung.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema
Ein beliebiger Punkt $P$ auf der Geraden $g$ hat die Koordinaten: $P (5 - 4 r | r | 1 + r)$
Ein beliebiger Punkt $Q$ auf der Geraden $h$ hat die Koordinaten: $Q (5 + 2 s | 3 + s | 7 - 2 s)$
Schritt 1
Der Punkt $Q \in h$ ist beliebig, aber mit konstantem $s$ . Der Punkt $P \in g$ ist beliebig und variabel mit dem Parameter r. Der Abstand $d = | \vec{P Q} |$ ist dann eine Funktion von $r$ $ \Rightarrow d = d (r)$ .
Berechne den Vektor $\vec{P Q} = \vec{O Q} - \vec{O P} = (\begin{array}{c} 5 + 2 s - (5 - 4 r) \\ 3 + s - r \\ 7 - 2 s - (1 + r) \end{array}) = (\begin{array}{c} 2 s + 4 r \\ 3 + s - r \\ 6 - 2 s - r \end{array})$
$(I) d = | \vec{P Q} | = \sqrt{(2 s + 4 r)^{2} + (3 + s - r)^{2} + (6 - 2 s - r)^{2}}$
Der Abstand $d$ zwischen $P$ und Q soll minimal werden.
Die Bedingung für ein Minimum lautet dann: $d (r)^{'} = 0$ und $d (r)^{''} > 0$ .
Zur Vereinfachung wird nicht die Funktion $d (r)$ abgeleitet sondern die Funktion $d^{*} (r) = (d (r))^{2}$ .
Damit entfällt die Ableitung der Wurzel. Wenn die Funktion $d^{*} (r)$ minimal ist, dann ist auch die Funktion $d (r)$ minimal.
$(II) d^{*} (r) = (d (r))^{2} = (2 s + 4 r)^{2} + (3 + s - r)^{2} + (6 - 2 s - r)^{2}$
Berechne die erste und zweite Ableitung der Funktion $d^{*} (r)$ .
$d^{*} (r)^{'} = 2 \cdot (2 s + 4 r) \cdot 4 + 2 \cdot (3 + s - r) \cdot (- 1) + 2 \cdot (6 - 2 s - r) \cdot (- 1)$
Beachte beim Ableiten die Kettenregel. Löse die Klammern auf und fasse zusammen:
$d^{*} (r)^{'} = 16 s + 32 r - 6 - 2 s + 2 r - 12 + 4 s + 2 r = - 18 + 18 s + 36 r$
$d^{*} (r)^{''} = 36 > 0$ Damit ist die Bedingung für ein Minimum erfüllt.
$d^{*} (r)^{'} = 0 \Rightarrow - 18 + 18 s + 36 r = 0$ nach $r$ aufgelöst folgt: $r = 0,5 - 0,5 s$
Schritt 2
Der Punkt $P_{F}$ wird nun als konstant betrachtet und der Punkt $Q$ ist variabel in Abhängigkeit von $s$ .
Der Abstand $d = | \vec{P Q} |$ ist dann eine Funktion von $s$ $ \Rightarrow d = d (s)$ .
Setze das berechnete $r = 0,5 - 0,5 s$ in Gleichung $(II)$ ein $\Rightarrow$
$d^{*} (s) = (2 s + 4 \cdot (0,5 - 0,5 s))^{2} + (3 + s - (0,5 - 0,5 s))^{2} + (6 - 2 s - (0,5 - 0,5 s))^{2}$
zusammengefasst erhältst du: $d^{*} (s) = = 4 + (2,5 + 1,5 s)^{2} + (5,5 - 1,5 s)^{2}$
Berechne die erste und zweite Ableitung der Funktion $d^{*} (s)$ .
$d^{*} (s)^{'} = 0 + 2 \cdot (2,5 + 1,5 s) \cdot 1,5 + 2 \cdot (5,5 - 1,5 s) \cdot (- 1,5)$
Beachte beim Ableiten die Kettenregel. Löse die Klammern auf und fasse zusammen:
$d^{*} (s)^{'} = 7,5 + 4,5 s - 16,5 + 4,5 s = - 9 + 9 s$
$d^{*} (s)^{''} = 9 > 0$ Damit ist die Bedingung für ein Minimum erfüllt.
$d^{*} (s)^{'} = 0 \Rightarrow - 9 + 9 s = 0$ mit der Lösung $s = 1$ .
Setze $s = 1$ in $r = 0,5 - 0,5 s$ ein, dann erhältst du für $r$ den Wert: $r = 0$
Setze $r$ und $s$ in Gleichung $(I)$ ein, dann gilt für den Abstand der beiden Geraden:
$d = \sqrt{(2 \cdot 1 + 4 \cdot 0)^{2} + (3 + 1 - 0)^{2} + (6 - 2 \cdot 1 - 0)^{2}} = \sqrt{4 + 16 + 16} = \sqrt{36} = 6$
Setze $r$ und $s$ in $P$ und $Q$ ein, dann erhältst du die beiden Lotfußpunkte:
$P_{F} (5 - 4 \cdot 0 | 0 | 1 + 0) \Rightarrow P_{F} (5 | 0 | 1)$ und $Q_{F} (5 + 2 \cdot 1 | 3 + 1 | 7 - 2 \cdot 1) \Rightarrow Q_{F} (7 | 4 | 5)$
Antwort: Die beiden windschiefen Geraden haben einen Abstand von $6 LE$ und die beiden Lotfußpunkte lauten $P_{F} (5 | 0 | 1)$ und $Q_{F} (7 | 4 | 5)$ .
5
Bestimme den Abstand zweier Ebenen mit Hilfe einer Lotgeraden.

Geben sind die beiden Ebenen:
$E_{1} : a x_{1} + b x_{2} + c x_{3} = d_{1}$
$E_{2} : a x_{1} + b x_{2} + c x_{3} = d_{2}$
Man erstellt die Gleichung einer Lotgeraden durch den Koordinatenursprung.
Der Richtungsvektor der Lotgeraden ist der Normalenvektor $\vec{n} = (\begin{array}{c} a \\ b \\ c \end{array})$ der Ebene.
$g_{L o t} : \vec{x} = r \cdot (\begin{array}{c} a \\ b \\ c \end{array})$
Man berechnet die beiden Schnittpunkte $S_{1}$ und $S_{2}$ der Lotgeraden mit den Ebenen $E_{1}$ und $E_{2}$ .
Der Abstand der beiden Ebenen ist dann der Betrag des Vektors $| \vec{S_{1} S_{2}} |$
Beispiel:
Geben sind die beiden Ebenen:
$E_{1} : x_{1} + 2 x_{2} + 2 x_{3} = 3$
$E_{2} : x_{1} + 2 x_{2} + 2 x_{3} = 6$
Der Normalenvektor der Ebene ist $\vec{n} = (\begin{array}{c} 1 \\ 2 \\ 2 \end{array})$ .
Die Lotgerade durch den Koordinatenursprung hat dann die Gleichung: $g_{L o t} : \vec{x} = r \cdot (\begin{array}{c} 1 \\ 2 \\ 2 \end{array})$
Man berechnet den Schnittpunkt von $g_{L o t}$ mit $E_{1}$ :
$g_{L o t} \cap E_{1} : r + 2 \cdot 2 r + 2 \cdot 2 r = 3 \Rightarrow 9 r = 3$ mit der Lösung $r = \frac{1}{3}$ .
Man setzt $r = \frac{1}{3}$ in $g_{L o t}$ ein und erhält den ersten Schnittpunkt:
${\vec{x}}_{S 1} = \frac{1}{3} \cdot (\begin{array}{c} 1 \\ 2 \\ 2 \end{array}) = (\begin{array}{c} \frac{1}{3} \\ \frac{2}{3} \\ \frac{2}{3} \end{array}) \Rightarrow S_{1} (\frac{1}{3} | \frac{2}{3} | \frac{2}{3})$
Man berechnet den Schnittpunkt von $g_{L o t}$ mit $E_{2}$ :
$g_{L o t} \cap E_{2} : r + 2 \cdot 2 r + 2 \cdot 2 r = 6 \Rightarrow 9 r = 6$ mit der Lösung $r = \frac{2}{3}$ .
Man setzt $r = \frac{2}{3}$ in $g_{L o t}$ ein und erhält den zweiten Schnittpunkt:

${\vec{x}}_{S 2} = \frac{2}{3} \cdot (\begin{array}{c} 1 \\ 2 \\ 2 \end{array}) = (\begin{array}{c} \frac{2}{3} \\ \frac{4}{3} \\ \frac{4}{3} \end{array}) \Rightarrow S_{2} (\frac{2}{3} | \frac{4}{3} | \frac{4}{3})$
Man berechnet den Vektor $\vec{S_{1} S_{2}}$ = $(\begin{array}{c} \frac{2}{3} \\ \frac{4}{3} \\ \frac{4}{3} \end{array}) - (\begin{array}{c} \frac{1}{3} \\ \frac{2}{3} \\ \frac{2}{3} \end{array}) = (\begin{array}{c} \frac{1}{3} \\ \frac{2}{3} \\ \frac{2}{3} \end{array})$ .
Man berechnet den Betrag des Vektors $\vec{S_{1} S_{2}}$ und erhält den Abstand der beiden Ebenen.
$d (E_{1}, E_{2}) = | \vec{S_{1} S_{2}} | = \sqrt{(\frac{1}{3})^{2} + (\frac{2}{3})^{2} + (\frac{2}{3})^{2}} = \sqrt{\frac{9}{9}} = 1$
Der Abstand der beiden Ebenen beträgt $1 LE$ .
6
Punkte in der Ebene

Gegeben ist eine Ebene $E : \vec{X} = \vec{A} + r \cdot \vec{u} + s \cdot \vec{v}$ (Parameterform mit den Parametern $r, s \in ℝ$ ). Wenn man für r und s beliebige Werte einsetzt, erhält man einen Punkt in der Ebene.
Beispiel
Man betrachtet die Ebene $E : \vec{X} = (\begin{array}{c} 2 \\ 5 \\ - 3 \end{array}) + r \cdot (\begin{array}{c} 5 \\ - 6 \\ - 9 \end{array}) + s \cdot (\begin{array}{c} 1 \\ 2 \\ 3 \end{array})$ und wählt z.B. für die beiden Parameter $r$ und $s$ die Werte $r = - 1$ und $s = 2$ . Diese beiden Werte beschreiben genau einen Punkt $P$ in der Ebene:
$\vec{P} = (\begin{array}{c} 2 \\ 5 \\ - 3 \end{array}) + (- 1) \cdot (\begin{array}{c} 5 \\ - 6 \\ - 9 \end{array}) + 2 \cdot (\begin{array}{c} 1 \\ 2 \\ 3 \end{array}) = (\begin{array}{c} - 1 \\ 15 \\ 12 \end{array})$
Der Punkt $P$ hat die Koordinaten: $P (- 1 | 15 | 12)$ und $P \in E$ .
Umgekehrt gibt es zu jedem Punkt in der Ebene passende Werte für die beiden Parameter $r$ und $s$ . Will man prüfen, ob ein Punkt $P$ in der Ebene liegt, wird der Ortvektor des Punktes $P$ mit der Ebenengleichung gleichgesetzt (man setzt für den Vektor $\vec{X}$ der Ebene den Ortvektor des Punktes $P$ ein).
Anschließend stellt man ein Gleichungssystem auf und löst die einzelnen Gleichungen nach $r$ und $s$ auf.
Verständlicher wird dies, wenn man sich Beispiele ansieht:
Beispiel 1
Gegeben ist die Ebenengleichung:
$E : \vec{X} = (\begin{array}{c} 2 \\ 5 \\ - 3 \end{array}) + r \cdot (\begin{array}{c} 5 \\ - 6 \\ - 9 \end{array}) + s \cdot (\begin{array}{c} 1 \\ 2 \\ 3 \end{array})$
Es soll geprüft werden, ob der Punkt $P (7 | - 1 | - 12)$ in der Ebene liegt.
Lösung für Beispiel 1
Man setzt für den Vektor $\vec{X}$ der Ebene $E$ den Ortvektor des Punktes $P (7 | - 1 | - 12)$ ein:
$(\begin{array}{c} 7 \\ - 1 \\ - 12 \end{array}) = (\begin{array}{c} 2 \\ 5 \\ - 3 \end{array}) + r \cdot (\begin{array}{c} 5 \\ - 6 \\ - 9 \end{array}) + s \cdot (\begin{array}{c} 1 \\ 2 \\ 3 \end{array})$
So erhält man ein Gleichungssystem mit drei Gleichungen und zwei Variablen.
$\begin{array}{llcr} (I) : & 7 & = & 2 + 5 \cdot r + 1 \cdot s \\ (I I) : & - 1 & = & 5 - 6 \cdot r + 2 \cdot s \\ (I I I) : & - 12 & = & - 3 - 9 \cdot r + 3 \cdot s \end{array}$
Umgeformt erhält man:
$\begin{array}{llcr} (I^{'}) : & 5 & = & 5 \cdot r + 1 \cdot s \\ (I I^{'}) : & - 6 & = & - 6 \cdot r + 2 \cdot s \\ (I I I^{'}) : & - 9 & = & - 9 \cdot r + 3 \cdot s \end{array}$
Um eine Variable zu eliminieren rechnet man z.B. $(- 2) \cdot (I^{'}) + (I I^{'})$
$\begin{array}{cccccccl} (- 2) \cdot (I^{'}) : & - 10 & = & - 10 \cdot r & - & 2 \cdot s \\ + (I I^{'}) : & - 6 & = & - 6 \cdot r & + & 2 \cdot s \end{array}$
$- 16 = - 16 \cdot r + 0 \Rightarrow r = 1$
Man setzt $r = 1$ in Gleichung $(I^{'}) : 5 = 5 \cdot r + 1 \cdot s$ ein:
$(I^{'}) : 5 = 5 \cdot 1 + 1 \cdot s \Rightarrow s = 0$

Mit den Werten $r = 1$ und $s = 0$ wird (als Probe) die Gleichung $(I I^{'}) : - 6 = - 6 \cdot r + 2 \cdot s$ überprüft:
$(I I^{'}) : - 6 = - 6 \cdot 1 + 2 \cdot 0 ✓$ Somit wurden $r$ und $s$ richtig berechnet.
Mit den Werten $r = 1$ und $s = 0$ wird die Gleichung $(I I I^{'}) : - 9 = - 9 \cdot r + 3 \cdot s$ überprüft:
$(I I I^{'}) : - 9 = - 9 \cdot 1 + 3 \cdot 0 ✓$
Damit hat das Gleichungssystem eine eindeutige Lösung, d.h. der Punkt $P$ liegt in der Ebene.
Beispiel 2
Gegeben ist die Ebenengleichung:
$E : \vec{X} = (\begin{array}{c} 2 \\ 5 \\ - 3 \end{array}) + r \cdot (\begin{array}{c} 5 \\ - 6 \\ - 9 \end{array}) + s \cdot (\begin{array}{c} 1 \\ 2 \\ 3 \end{array})$
Es soll geprüft werden, ob der Punkt $Q (4 | 10 | - 6)$ in der Ebene liegt.
Lösung für Beispiel 2
Man setzt für den Vektor $\vec{X}$ der Ebene $E$ den Ortvektor des Punktes $Q (4 | 10 | - 6)$ ein:
$(\begin{array}{c} 4 \\ 10 \\ - 6 \end{array}) = (\begin{array}{c} 2 \\ 5 \\ - 3 \end{array}) + r \cdot (\begin{array}{c} 5 \\ - 6 \\ - 9 \end{array}) + s \cdot (\begin{array}{c} 1 \\ 2 \\ 3 \end{array})$
So erhält man ein Gleichungssystem mit drei Gleichungen und zwei Variablen.
$\begin{array}{llcr} (I) : & 4 & = & 2 + 5 \cdot r + 1 \cdot s \\ (I I) : & 10 & = & 5 - 6 \cdot r + 2 \cdot s \\ (I I I) : & - 6 & = & - 3 - 9 \cdot r + 3 \cdot s \end{array}$
Umgeformt erhält man:
$\begin{array}{llcr} (I^{'}) : & 2 & = & 5 \cdot r + 1 \cdot s \\ (I I^{'}) : & 5 & = & - 6 \cdot r + 2 \cdot s \\ (I I I^{'}) : & - 3 & = & - 9 \cdot r + 3 \cdot s \end{array}$
Um eine Variable zu eliminieren rechnet man z.B. $(- 2) \cdot (I^{'}) + (I I^{'})$
$\begin{array}{cccccccl} (- 2) \cdot (I^{'}) : & - 4 & = & - 10 \cdot r & - & 2 \cdot s \\ + (I I^{'}) : & 5 & = & - 6 \cdot r & + & 2 \cdot s \end{array}$
$1 = - 16 \cdot r + 0 \Rightarrow r = - \frac{1}{16}$
Man setzt $r = - \frac{1}{16}$ in Gleichung $(I^{'}) : 2 = 5 \cdot r + 1 \cdot s$ ein:
$(I^{'}) : 2 = 5 \cdot (- \frac{1}{16}) + 1 \cdot s \Rightarrow s = \frac{37}{16}$ .
Mit den Werten $r = - \frac{1}{16}$ und $s = \frac{37}{16}$ wird (als Probe) die Gleichung $(I I^{'}) : 5 = - 6 \cdot r + 2 \cdot s$ überprüft:
$(I I^{'}) : 5 = - 6 \cdot (- \frac{1}{16}) + 2 \cdot \frac{37}{16} = \frac{6}{16} + \frac{74}{16} = \frac{80}{16} = 5 ✓$ Somit wurden $r$ und $s$ richtig berechnet.
Mit den Werten $r = - \frac{1}{16}$ und $s = \frac{37}{16}$ wird die Gleichung $(I I I^{'}) : - 3 = - 9 \cdot r + 3 \cdot s$ überprüft:
$(I I I^{'}) : - 3 = - 9 \cdot (- \frac{1}{16}) + 3 \cdot \frac{37}{16} = \frac{9}{16} + \frac{111}{16} = \frac{120}{16} = 7,5$
Gleichung $(I I I^{'})$ liefert ein falsches Ergebnis, da $- 3 \neq 7,5$ .
Das Gleichungssystem hat keine Lösung, d.h. der Punkt $Q$ liegt nicht in der Ebene.
7
Testlösungen Abitur BW

Aufgabe 6.1
$\begin{array}{rccccccc} I & x_{1} & + & x_{2} & + & 7 x_{3} & = & 2 \\ II & 2 x_{1} & - & x_{2} & - & 3 x_{3} & = & - 5 \\ III & 4 x_{1} & - & x_{2} & + & 4 x_{3} & = & - 7 \end{array} $
Zunächst solltest du es zu einer erweiterten Koeffizientenmatrix umschreiben:
$(\begin{array}{rrrc} 1 & 1 & 7 & 2 \\ 2 & - 1 & - 3 & - 5 \\ 4 & - 1 & 4 & - 7 \end{array})$
Als ersten Schritt des Gaußverfahrens verwendest du jetzt das Additionsverfahren, um die beiden Einträge, die jetzt $orange$ markiert sind auf null zu bringen.
$\begin{array}{c} (\begin{array}{rrrc} 1 & 1 & 7 & 2 \\ 2 & - 1 & - 3 & - 5 \\ 4 & - 1 & 4 & - 7 \end{array}) & \underset{\to}{II - 2 \cdot I} & (\begin{array}{rrrc} 1 & 1 & 7 & 2 \\ 0 & - 3 & - 17 & - 9 \\ 4 & - 1 & 4 & - 7 \end{array}) \\ (\begin{array}{rrrc} 1 & 1 & 7 & 2 \\ 0 & - 3 & - 17 & - 9 \\ 4 & - 1 & 4 & - 7 \end{array}) & \underset{\to}{III - 4 \cdot I} & (\begin{array}{rrrc} 1 & 1 & - 7 & 2 \\ 0 & - 3 & - 17 & - 9 \\ 0 & - 5 & - 24 & - 15 \end{array}) \end{array}$
Dazu ziehst du von der zweiten Zeile das Doppelte der ersten Zeile ab $(II - 2 \cdot I)$ .
Anschließend ziehst du von der dritten Zeile das Vierfache der ersten Zeile ab $(III - 4 \cdot I)$ .
Jetzt gibt es in deiner erweiterten Koeffizientenmatrix nur noch einen Eintrag unter der Diagonalen, der nicht null ist, in der Matrix ist er $grün$ markiert.
Damit auch in diesem Eintrag der Matrix eine null steht, addierst du nun zum minus Dreifachen der dritten Zeile das Fünffache der zweiten Zeile $(- 3 \cdot III + 5 \cdot II)$ .

$\begin{array}{c} (\begin{array}{rrrc} 1 & 1 & - 7 & 2 \\ 0 & - 3 & - 17 & - 9 \\ 0 & - 5 & - 24 & - 15 \end{array}) & \underset{\to}{- 3 \cdot III + 5 \cdot II} & (\begin{array}{rrrc} 1 & 1 & - 7 & 2 \\ 0 & - 3 & - 17 & - 9 \\ 0 & 0 & - 13 & 0 \end{array}) \end{array}$
Die letzte Zeile lautet nun: $- 13 x_{3} = 0 \Rightarrow x_{3} = 0$
Aus Zeile $2$ folgt dann mit $x_{3} = 0$ : $- 3 x_{2} - 17 \cdot 0 = - 9 \Rightarrow x_{2} = 3$
Aus Zeile $1$ folgt dann mit $x_{3} = 0$ und $x_{2} = 3$ : $x_{1} + 3 - 7 \cdot 0 = 2 \Rightarrow x_{1} = - 1$
Antwort: Das lineare Gleichungssystem hat die Lösungsmenge $𝕃 = {(- 1 | 3 | 0}$
Aufgabe 6.2
Du machst den Ansatz: $\vec{v} = r \cdot \vec{a} + s \cdot \vec{b} + t \cdot \vec{c}$
$(\begin{array}{c} 14 \\ - 5 \\ 7 \end{array}) = r \cdot (\begin{array}{c} 0 \\ 1 \\ 3 \end{array}) + s \cdot (\begin{array}{c} - 1 \\ 3 \\ 7 \end{array}) + t \cdot (\begin{array}{c} 5 \\ - 2 \\ 2 \end{array})$
Um das Gaußverfahren anzuwenden, sollte in der erweiterten Koeffizientenmatrix an der ersten Stelle keine $0$ stehen. Deshalb werden die Spalten $1$ und $2$ vertauscht.
$(\begin{array}{rrrc} - 1 & 0 & 5 & 14 \\ 3 & 1 & - 2 & - 5 \\ 7 & 3 & 2 & 7 \end{array})$
Als ersten Schritt des Gaußverfahrens verwendest du jetzt das Additionsverfahren, um die beiden Einträge, die jetzt $orange$ markiert sind auf null zu bringen.
$\begin{array}{c} (\begin{array}{rrrc} - 1 & 0 & 5 & 14 \\ 3 & 1 & - 2 & - 5 \\ 7 & 3 & 2 & 7 \end{array}) & \underset{\to}{II + 3 \cdot I} & (\begin{array}{rrrc} - 1 & 0 & 5 & 14 \\ 0 & 1 & 13 & 37 \\ 7 & 3 & 2 & 7 \end{array}) \\ (\begin{array}{rrrc} - 1 & 0 & 5 & 14 \\ 0 & 1 & 13 & 37 \\ 7 & 3 & 2 & 7 \end{array}) & \underset{\to}{III + 7 \cdot I} & (\begin{array}{rrrc} - 1 & 0 & 5 & 14 \\ 0 & 1 & 13 & 37 \\ 0 & 3 & 37 & 105 \end{array}) \end{array}$
Dazu addierst du zur zweiten Zeile das Dreifache der ersten Zeile $(II + 3 \cdot I)$ .
Anschließend addierst du zur dritten Zeile das Siebenfache der ersten Zeile $(III + 7 \cdot I)$ .
Jetzt gibt es in deiner erweiterten Koeffizientenmatrix nur noch einen Eintrag unter der Diagonalen, der nicht null ist, in der Matrix ist er $grün$ markiert.
Damit auch in diesem Eintrag der Matrix eine null steht, subtrahierst du das Dreifache der zweiten Zeile von der dritten Zeile $(III - 3 \cdot II)$ .

$\begin{array}{c} (\begin{array}{rrrc} - 1 & 0 & 5 & 14 \\ 0 & 1 & 13 & 37 \\ 0 & 3 & 37 & 105 \end{array}) & \underset{\to}{III - 3 \cdot II} & (\begin{array}{rrrc} - 1 & 0 & 5 & 14 \\ 0 & 1 & 13 & 37 \\ 0 & 0 & - 2 & - 6 \end{array}) \end{array}$
Die letzte Zeile lautet nun: $- 2 \cdot t = - 6 \Rightarrow t = 3$
Aus Zeile $2$ folgt dann mit $t = 3$ : $r + 13 \cdot 3 = 37 \Rightarrow r = - 2$
Aus Zeile $1$ folgt dann mit $t = 3$ und $r = - 2$ : $- s + 0 \cdot (- 2) + 5 \cdot 3 = 14 \Rightarrow s = 1$
Antwort: Der Vektor $\vec{v}$ kann durch die folgende Linearkombination dargestellt werden:
$(\begin{array}{c} 14 \\ - 5 \\ 7 \end{array}) = (- 2) \cdot (\begin{array}{c} 0 \\ 1 \\ 3 \end{array}) + 1 \cdot (\begin{array}{c} - 1 \\ 3 \\ 7 \end{array}) + 3 \cdot (\begin{array}{c} 5 \\ - 2 \\ 2 \end{array})$
Aufgabe 6.3
Lösung zu a)
Die rote Ebene ist die Ebene $E_{1}$ in Koordinatenform: $2 x_{1} + 3 x_{2} + 2 x_{3} = 12$
In Achsenabschnittsform lautet $E_{1}$ : $\frac{x_{1}}{6} + \frac{x_{2}}{4} + \frac{x_{3}}{6} = 1$
So können die Achsenschnittpunkte (Spurpunkte) abgelesen werden: $S_{x_{1}} (6 | 0 | 0)$ ; $S_{x_{2}} (0 | 4 | 0)$ ; $S_{x_{3}} (0 | 0 | 6)$
Die grüne Ebene ist die Ebene $E_{2}$ : $x_{3} = 2$ . Sie hat den Achsenschnittpunkt $S_{x_{3}} (0 | 0 | 2)$ und sie liegt parallel zur $x_{1}$ - $x_{2}$ -Ebene.
Lösung zu b)
Du suchst zwei Punkte, die in beiden Ebenen liegen.
Für alle Werte von $x_{1}$ liegt der Punkt $A (x_{1} | 0 | 2)$ in der Ebene $E_{2}$ ( $A$ erfüllt die Ebenengleichung).
Für alle Werte von $x_{2}$ liegt der Punkt $B (0 | x_{2} | 2)$ in der Ebene $E_{2}$ ( $B$ erfüllt die Ebenengleichung).
Die Punkte $A$ und $B$ sollen gemeinsame Punkte der beiden Ebenen sein. Deshalb müssen beide Punkte auch die Ebenengleichung $E_{1}$ erfüllen.
$A \in E_{1} \Rightarrow 2 \cdot x_{1} + 3 \cdot 0 + 2 \cdot 2 = 12 \Rightarrow x_{1} = 4 \Rightarrow A (4 | 0 | 2)$
$B \in E_{1} \Rightarrow 2 \cdot 0 + 3 \cdot x_{2} + 2 \cdot 2 = 12 \Rightarrow x_{2} = \frac{8}{3} \Rightarrow B (0 | \frac{8}{3} | 2)$
Die Schnittgerade ergibt sich dann zu: $g : \vec{X} = \vec{O A} + r \cdot \vec{A B}$
$g : \vec{X} = (\begin{array}{c} 4 \\ 0 \\ 2 \end{array}) + r \cdot ((\begin{array}{c} 0 \\ \frac{8}{3} \\ 2 \end{array}) - (\begin{array}{c} 4 \\ 0 \\ 2 \end{array})) = (\begin{array}{c} 4 \\ 0 \\ 2 \end{array}) + r \cdot (\begin{array}{c} - 4 \\ \frac{8}{3} \\ 0 \end{array})$
Der Richtungsvektor kann noch vereinfacht werden: $(\begin{array}{c} - 4 \\ \frac{8}{3} \\ 0 \end{array}) \underset{\to}{\cdot 3} (\begin{array}{c} - 12 \\ 8 \\ 0 \end{array}) \underset{\to}{: 4} (\begin{array}{c} - 3 \\ 2 \\ 0 \end{array})$
Antwort: Die Gleichung der Schnittgeraden lautet: $g : \vec{X} = (\begin{array}{c} 4 \\ 0 \\ 2 \end{array}) + r \cdot (\begin{array}{c} - 3 \\ 2 \\ 0 \end{array})$
Aufgabe 6.4
Lösung zu a)
Die grüne Ebene ist die Ebene $E$ in Koordinatenform: $x_{1} + 2 x_{2} = 4$
In Achsenabschnittsform lautet $E$ : $\frac{x_{1}}{4} + \frac{x_{2}}{2} = 1$
So können die Achsenschnittpunkte (Spurpunkte) abgelesen werden: $S_{x_{1}} (4 | 0 | 0)$ ; $S_{x_{2}} (0 | 2 | 0)$
Es gibt keinen Schnittpunkt mit der $x_{3}$ -Achse, d.h. die Ebene $E$ verläuft parallel zur $x_{3}$ -Achse
Die rote Ebene ist die Ebene $F$ in Koordinatenform: $2 x_{1} + x_{2} + 2 x_{3} = 8$
In Achsenabschnittsform lautet $F$ : $\frac{x_{1}}{4} + \frac{x_{2}}{8} + \frac{x_{3}}{4} = 1$
So können die Achsenschnittpunkte abgelesen werden: $S_{x_{1}} (4 | 0 | 0)$ ; $S_{x_{2}} (0 | 8 | 0)$ ; $S_{x_{3}} (0 | 0 | 4)$
Lösung zu b)
Du suchst zwei Punkte, die in beiden Ebenen liegen.
Der Punkt $A (4 | 0 | 0) = S_{x_{1}}$ ist ein gemeinsamer Punkt der beiden Ebenen $E$ und $F$ .
Für alle Werte von $x_{3}$ liegt der Punkt $B (0 | 2 | x_{3})$ in der Ebene $E$ ( $B$ erfüllt die Ebenengleichung).
Damit $B$ auch in der Ebene $F$ liegt, muss gelten:
$B \in F \Rightarrow 2 \cdot 0 + 2 + 2 \cdot x_{3} = 8 \Rightarrow x_{3} = 3 \Rightarrow B (0 | 2 | 3)$
Die Schnittgerade ergibt sich dann zu: $g : \vec{X} = \vec{O A} + r \cdot \vec{A B}$
$g : \vec{X} = (\begin{array}{c} 4 \\ 0 \\ 0 \end{array}) + r \cdot ((\begin{array}{c} 0 \\ 2 \\ 3 \end{array}) - (\begin{array}{c} 4 \\ 0 \\ 0 \end{array})) = (\begin{array}{c} 4 \\ 0 \\ 0 \end{array}) + r \cdot (\begin{array}{c} - 4 \\ 2 \\ 3 \end{array})$
Antwort: Die Gleichung der Schnittgeraden lautet: $g : \vec{X} = (\begin{array}{c} 4 \\ 0 \\ 2 \end{array}) + r \cdot (\begin{array}{c} - 4 \\ 2 \\ 3 \end{array})$
Aufgabe 6.5
Lösung zu a)
Die Ebene $E$ hat keinen Schnittpunkt mit der $x_{1}$ -Achse, d.h. die Ebenengleichung $E$ hat unter Berücksichtigung der gegebenen Spurpunkte die Achsenabschnittsform:
$E : \frac{x_{2}}{- 3} + \frac{x_{3}}{4} = 1 \Rightarrow - 4 x_{2} + 3 x_{3} = 12$
Antwort: Die Gleichung der Ebene $E$ lautet: $- 4 x_{2} + 3 x_{3} = 12$
Lösung zu b)
Die Ebene $E$ hat den Normalenvektor ${\vec{n}}_{E} = (\begin{array}{c} 1 \\ 0 \\ 0 \end{array})$ .
Da die Ebene $F$ parallel zu $E$ sein soll, hat sie den gleichen Normalenvektor wie $E$ und enthält den Punkt A.
$F : (\vec{x} - \vec{O A}) \circ {\vec{n}}_{E} = 0 \Rightarrow (\vec{x} - (\begin{array}{c} 3 \\ - 3 \\ - 1 \end{array})) \circ (\begin{array}{c} 1 \\ 0 \\ 0 \end{array}) = 0 \Rightarrow x_{1} - 3 = 0$
Antwort: Die Gleichung der Ebene $F$ lautet: $x_{1} = 3$ .
Lösung zu c)
Der Normalenvektor $\vec{n} = (\begin{array}{c} - 2 \\ 1 \\ 0 \end{array})$ der gegebenen Ebene $E$ ist der Richtungsvektor der Geraden $g$ ,
da die Gerade senkrecht zu $E$ steht.
Als Aufpunkt der Geraden $g$ wird der Punkt $P$ genommen.
Antwort: Die Gleichung der Geraden $g$ lautet: $\vec{X} = (\begin{array}{c} 5 \\ 1 \\ - 4 \end{array}) + r \cdot (\begin{array}{c} - 2 \\ 1 \\ 0 \end{array})$
Aufgabe 6.6
Lösung zu a)
Wenn die beiden Richtungsvektoren Vielfache voneinander sind, dann gilt $g ∥ h$ :
${\vec{u}}_{g} = (\begin{array}{c} 3 \\ - 1 \\ 5 \end{array})$ und ${\vec{u}}_{h} = (\begin{array}{c} - 9 \\ 3 \\ - 15 \end{array})$ $\Rightarrow {\vec{u}}_{h} = (- 3) \cdot {\vec{u}}_{g} \Rightarrow g ∥ h$
Der Aufpunkt der Geraden $g$ liegt nicht auf der Geraden $h$ , denn:
$(\begin{array}{c} 4 \\ - 1 \\ 0 \end{array}) = (\begin{array}{c} 4 \\ - 1 \\ 1 \end{array}) + r \cdot (\begin{array}{c} - 9 \\ 3 \\ - 15 \end{array}) \Rightarrow (\begin{array}{c} 0 \\ 0 \\ - 1 \end{array}) \neq r \cdot (\begin{array}{c} - 9 \\ 3 \\ - 15 \end{array})$
Die letzte Gleichung ist für kein $r$ erfüllbar.
Antwort: Die beiden Geraden sind parallel, aber nicht identisch.
Lösung zu b)
Die gesuchte Ebene hat als Aufpunkt den Aufpunkt der Geraden $g$ und als einen Richtungsvektor den Richtungsvektor der Geraden $g$ . Einen zweiten Richtungsvektor der Ebene $E$ erhältst du als Differenz der beiden Aufpunkte der Geraden $g$ und $h$ .
$E : \vec{x} = (\begin{array}{c} 4 \\ - 1 \\ 0 \end{array}) + r \cdot (\begin{array}{c} 3 \\ - 1 \\ 5 \end{array}) + s \cdot ((\begin{array}{c} 4 \\ - 1 \\ 1 \end{array}) - (\begin{array}{c} 4 \\ - 1 \\ 0 \end{array})) = (\begin{array}{c} 4 \\ - 1 \\ 0 \end{array}) + r \cdot (\begin{array}{c} 3 \\ - 1 \\ 5 \end{array}) + s \cdot (\begin{array}{c} 0 \\ 0 \\ 1 \end{array})$
Antwort: Die Gleichung der Ebene $E$ lautet: $\vec{x} = (\begin{array}{c} 4 \\ - 1 \\ 0 \end{array}) + r \cdot (\begin{array}{c} 3 \\ - 1 \\ 5 \end{array}) + s \cdot (\begin{array}{c} 0 \\ 0 \\ 1 \end{array})$
Aufgabe 7.1
Lösung zu a)
Die Ebenen sind parallel zueinander, wenn die Normalenvektoren parallel zueinander sind.
$\vec{a} \times \vec{b} = (\begin{array}{c} a_{2} b_{3} - a_{3} b_{2} \\ a_{3} b_{1} - a_{1} b_{3} \\ a_{1} b_{2} - a_{2} b_{1} \end{array}) \Rightarrow {\vec{n}}_{E} = (\begin{array}{c} - 1 \\ 0 \\ 1 \end{array}) \times (\begin{array}{c} 1 \\ - 1 \\ - 2 \end{array}) = (\begin{array}{c} 1 \\ - 1 \\ 1 \end{array})$
Aus der Koordinatenform von der Ebene $F$ liest du den Normalenvektor ab:
${\vec{n}}_{F} = (\begin{array}{c} 1 \\ - 1 \\ 1 \end{array}) \Rightarrow {\vec{n}}_{E} = {\vec{n}}_{F}$
Die Ebenen sind parallel zueinander.
Lösung zu b)
Erstelle die Hessesche Normalenform der Ebene $F$ :
$F_{H N F} : \frac{a x_{1} + b x_{2} + c x_{3} + d}{\sqrt{a^{2} + b^{2} + c^{2}}} = 0 \Rightarrow \frac{x_{1} - x_{2} + x_{3} - 1}{\sqrt{3}} = 0$
Setze den Aufpunkt $A (1 | 2 | 3)$ der Ebene $E$ in die Hessesche Normalenform ein, um den Abstand der beiden Ebenen zu berechnen.
$d (A, F) = | \frac{1 \cdot 1 - 1 \cdot 2 + 1 \cdot 3 - 1}{\sqrt{1^{2} + (- 1)^{2} + 1^{2}}} | = | \frac{1}{\sqrt{3}} | = \frac{1}{\sqrt{3}} = \frac{1}{3} \cdot \sqrt{3}$
Antwort: Die beiden Ebenen haben einen Abstand von $\frac{1}{3} \cdot \sqrt{3}$ voneinander.
Aufgabe 7.2
Lösung zu a)
Für die Ebene in Parameterform gilt:
$E_{A B C} = \vec{O A} + r \cdot (\vec{O B} - \vec{O A}) + s \cdot (\vec{O C} - \vec{O A})$
$E_{A B C} = (\begin{array}{c} 3 \\ 0 \\ 1 \end{array}) + r \cdot ((\begin{array}{c} 6 \\ 2 \\ 2 \end{array}) - (\begin{array}{c} 3 \\ 0 \\ 1 \end{array})) + s \cdot ((\begin{array}{c} 0 \\ 3 \\ 5 \end{array}) - (\begin{array}{c} 3 \\ 0 \\ 1 \end{array}))$
$E_{A B C} = (\begin{array}{c} 3 \\ 0 \\ 1 \end{array}) + r \cdot (\begin{array}{c} 3 \\ 2 \\ 1 \end{array}) + s \cdot (\begin{array}{c} - 3 \\ 3 \\ 4 \end{array})$
Bei der Umrechnung der Ebenengleichung in die Normalenform muss das Kreuzprodukt der beiden Richtungsvektoren der Ebene berechnet werden.
${\vec{n}}_{E} = (\begin{array}{c} 3 \\ 2 \\ 1 \end{array}) \times (\begin{array}{c} - 3 \\ 3 \\ 4 \end{array}) = (\begin{array}{c} 5 \\ - 15 \\ 15 \end{array})$
Der Normalenvektor kann noch vereinfacht werden: ${\vec{n}}_{E} = (\begin{array}{c} 1 \\ - 3 \\ 3 \end{array})$
Mit dem Punkt $A (3 | 0 | 1)$ erhältst du dann die Normalenform der Ebene:
$E : (\vec{x} - \vec{O A}) \circ {\vec{n}}_{E} = 0 \Rightarrow (\vec{x} - (\begin{array}{c} 3 \\ 0 \\ 1 \end{array})) \circ (\begin{array}{c} 1 \\ - 3 \\ 3 \end{array}) = 0$
Wird das Skalarprodukt ausmultipliziert, erhältst du die Koordinatenform der Ebenengleichung:
$E : x_{1} - 3 x_{2} + x_{3} - (3 + 0 + 3) = 0 \Rightarrow x_{1} - 3 x_{2} + x_{3} - 6 = 0$
Antwort: Die Ebene in Normalenform hat die Gleichung $E : (\vec{x} - (\begin{array}{c} 3 \\ 0 \\ 1 \end{array})) \circ (\begin{array}{c} 1 \\ - 3 \\ 3 \end{array}) = 0$ und in Koordinatenform lautet sie: $E : x_{1} - 3 x_{2} + x_{3} = 6$
Lösung zu b)
Lageuntersuchung: $g \cap E$
Setze $g$ in $E$ ein:
$(4 + 2 t) - 3 (t) + 3 (1)$ $=$ $6$
↓
Löse die Klammern auf
$4 + 2 t - 3 t + 3$ $=$ $6$
↓
Löse nach $t$ auf.
$7 - t$ $=$ $6$ $- 7$
$- t$ $=$ $- 1$ $\cdot (- 1)$
$t$ $=$ $1$
Du hast für $t$ eine Lösung erhalten, d.h. die Gerade und die Ebene schneiden sich.
Berechnung des Schnittpunktes der Geraden mit der Ebene
Setze $t = 1$ in die Geradengleichung ein: ${\vec{x}}_{S} = (\begin{array}{c} 4 \\ 0 \\ 1 \end{array}) + 1 \cdot (\begin{array}{c} 2 \\ 1 \\ 0 \end{array}) = (\begin{array}{c} 6 \\ 1 \\ 1 \end{array})$
Antwort: Die Gerade $g$ schneidet die Ebene $E$ im Punkt $S (6 | 1 | 1)$ .
Aufgabe 7.3
Lösung zu a)
Wenn die Geraden $g$ und $h$ orthogonal zueinander liegen sollen, dann muss das Skalarprodukt ihrer Richtungsvektoren gleich null sein.
${\vec{u}}_{g} = (\begin{array}{c} 2 \\ 1 \\ - 4 \end{array})$ und ${\vec{u}}_{h} = (\begin{array}{c} 1 \\ 2 \\ 1 \end{array})$ $\Rightarrow {\vec{u}}_{g} \circ {\vec{u}}_{h} = (\begin{array}{c} 2 \\ 1 \\ - 4 \end{array}) \circ (\begin{array}{c} 1 \\ 2 \\ 1 \end{array}) = 2 + 2 - 4 = 0$
Antwort: Die Geraden $g$ und $h$ liegen orthogonal zueinander.
Lösung zu b)
Lageuntersuchung:
Setze $g = h$ :
$(\begin{array}{c} 3 \\ - 2 \\ 7 \end{array}) + t \cdot (\begin{array}{c} 2 \\ 1 \\ - 4 \end{array}) = (\begin{array}{c} 7 \\ 3 \\ 5 \end{array}) + s \cdot (\begin{array}{c} 1 \\ 2 \\ 1 \end{array})$
Umgeformt erhältst du: $(\begin{array}{c} 3 \\ - 2 \\ 7 \end{array}) - (\begin{array}{c} 7 \\ 3 \\ 5 \end{array}) = s \cdot (\begin{array}{c} 1 \\ 2 \\ 1 \end{array}) - t \cdot (\begin{array}{c} 2 \\ 1 \\ - 4 \end{array})$ bzw.
$(\begin{array}{c} - 4 \\ - 5 \\ 2 \end{array}) = s \cdot (\begin{array}{c} 1 \\ 2 \\ 1 \end{array}) - t \cdot (\begin{array}{c} 2 \\ 1 \\ - 4 \end{array})$
Damit ergibt sich folgendes Gleichungssystem:
$\begin{array}{rccccccc} I & s & - & 2 t & = & - 4 \\ II & 2 s & - & t & = & - 5 \\ III & s & + & 4 t & = & 2 \end{array} $
Mit dem Additionsverfahren wird aus den Gleichungen $(I)$ und $(I I)$ der Parameter $s$ eliminiert.
Rechne dazu: $II + (- 2) \cdot I$ $\Rightarrow 3 t = 3 \Rightarrow t = 1$
Setze $t = 1$ in Gleichung $(I)$ ein $\Rightarrow s - 2 \cdot 1 = - 4 \Rightarrow s = - 2$
Probe in Gleichung $(I I I)$ : $s + 4 t = 2 \Rightarrow - 2 + 4 \cdot 1 = 2 ✓$
Zur Berechnung des Schnittpunktes setze $t = 1$ in die Geradengleichung $g$ ein:
${\vec{x}}_{S} = (\begin{array}{c} 3 \\ - 2 \\ 7 \end{array}) + 1 \cdot (\begin{array}{c} 2 \\ 1 \\ - 4 \end{array}) = (\begin{array}{c} 5 \\ - 1 \\ 3 \end{array})$
Antwort: Die Geraden $g$ und $h$ schneiden sich im Punkt $S (5 | - 1 | 3)$ .
Aufgabe 7.4
Lösung zu a)
Wenn das Dreieck rechtwinklig ist, mit rechtem Winkel im Punkt $C$ , dann muss das Skalarprodukt $\vec{B C} \circ \vec{C A} = 0$ sein. Berechne die Vektoren $\vec{B C}$ und $\vec{C A}$ :
$\vec{B C} = (\begin{array}{c} 2 \\ 8 \\ 4 \end{array}) - (\begin{array}{c} 4 \\ 10 \\ 5 \end{array}) = (\begin{array}{c} - 2 \\ - 2 \\ - 1 \end{array})$
$\vec{C A} = (\begin{array}{c} 12 \\ 0 \\ 0 \end{array}) - (\begin{array}{c} 2 \\ 8 \\ 4 \end{array}) = (\begin{array}{c} 10 \\ - 8 \\ - 4 \end{array})$
Berechne das Skalarprodukt: $\vec{B C} \circ \vec{C A} = (\begin{array}{c} - 2 \\ - 2 \\ - 1 \end{array}) \circ (\begin{array}{c} 10 \\ - 8 \\ - 4 \end{array}) = - 20 + 16 + 4 = 0 ✓$
Antwort: Das Dreieck hat im Punkt $C$ einen rechten Winkel.
Lösung zu b)
Die Dreiecksfläche berechnet sich dann zu:
$A = \frac{1}{2} \cdot | \vec{B C} | \cdot | \vec{C A} | = \frac{1}{2} \cdot \sqrt{(- 2)^{2} + (- 2)^{2} + (- 1)^{2}} \cdot \sqrt{10^{2} + (- 8)^{2} + (- 4)^{2}} = \frac{1}{2} \cdot \sqrt{9} \cdot \sqrt{180} = \frac{3}{2} \cdot \sqrt{180} = \frac{3}{2} \cdot 6 \cdot \sqrt{5} = 9 \cdot \sqrt{5}$
Antwort: Das Dreieck hat einen Flächeninhalt von $9 \cdot \sqrt{5} FE$ .
Aufgabe 7.5
Für ein beliebiges Dreieck gilt die folgende Flächenformel: $A = \frac{1}{2} \cdot \sqrt{{\vec{a}}^{2} \cdot {\vec{b}}^{2} - (\vec{a} \circ \vec{b})^{2}}$
$\vec{a} = \vec{A B} = (\begin{array}{c} 3 \\ 7 \\ - 4 \end{array}) - (\begin{array}{c} 1 \\ 3 \\ 0 \end{array}) = (\begin{array}{c} 2 \\ 4 \\ - 4 \end{array})$
$\vec{b} = \vec{A C} = (\begin{array}{c} 2 \\ 8 \\ 1 \end{array}) - (\begin{array}{c} 1 \\ 3 \\ 0 \end{array}) = (\begin{array}{c} 1 \\ 5 \\ 1 \end{array})$
Eingesetzt in die Flächenformel:
$A = \frac{1}{2} \cdot \sqrt{{(\begin{array}{c} 2 \\ 4 \\ - 4 \end{array})}^{2} \cdot {(\begin{array}{c} 1 \\ 5 \\ 1 \end{array})}^{2} - {((\begin{array}{c} 2 \\ 4 \\ - 4 \end{array}) \circ (\begin{array}{c} 1 \\ 5 \\ 1 \end{array}))}^{2}}$
$A = \frac{1}{2} \cdot \sqrt{(4 + 16 + 16) \cdot (1 + 25 + 1) - (2 + 20 - 4)^{2}}$
$A = \frac{1}{2} \cdot \sqrt{36 \cdot 27 - 18^{2}} = \frac{1}{2} \cdot \sqrt{648} = \frac{1}{2} \cdot 18 \cdot \sqrt{2} = 9 \cdot \sqrt{2}$
Antwort: Das Dreieck hat einen Flächeninhalt von $9 \cdot \sqrt{2} FE$ .
Aufgabe 7.6
Lösung zu a)
Berechne die Beträge der Vektoren $\vec{A B}$ , $\vec{B C}$ und $\vec{A C}$
$\vec{A B} = (\begin{array}{c} - 5 \\ 3 \\ 1 \end{array}) - (\begin{array}{c} - 7 \\ 0 \\ 1 \end{array}) = (\begin{array}{c} 2 \\ 3 \\ 0 \end{array}) \Rightarrow | \vec{A B} | = | (\begin{array}{c} 2 \\ 3 \\ 0 \end{array}) | = \sqrt{2^{2} + 3^{2} + 0^{2}} = \sqrt{13}$
$\vec{B C} = (\begin{array}{c} - 4 \\ 0 \\ - 1 \end{array}) - (\begin{array}{c} - 5 \\ 3 \\ 1 \end{array}) = (\begin{array}{c} 1 \\ - 3 \\ - 2 \end{array}) \Rightarrow | \vec{A B} | = | (\begin{array}{c} 1 \\ - 3 \\ - 2 \end{array}) | = \sqrt{1^{2} + (- 3)^{2} + (- 2)^{2}} = \sqrt{14}$
$\vec{A C} = (\begin{array}{c} - 4 \\ 0 \\ - 1 \end{array}) - (\begin{array}{c} - 7 \\ 0 \\ 1 \end{array}) = (\begin{array}{c} 3 \\ 0 \\ - 2 \end{array}) \Rightarrow | \vec{A B} | = | (\begin{array}{c} 3 \\ 0 \\ - 2 \end{array}) | = \sqrt{3^{2} + 0^{2} + (- 2)^{2}} = \sqrt{13}$
$| \vec{A B} | = | \vec{A C} | \neq | \vec{B C} |$ , d.h. das Dreieck ist gleichschenklig, mit der Basis $[B C]$ .
Lösung zu b)
$[B C]$ ist die Basis des gleichschenkligen Dreiecks, d.h. der Punkt $P$ muss $A$ gegenüberliegen; siehe Skizze.
Du kannst die folgende Vektorgleichung aufstellen, um $P$ zu berechnen.
$\vec{O P} = \vec{O C} + \vec{A B} = (\begin{array}{c} - 4 \\ 0 \\ - 1 \end{array}) + (\begin{array}{c} 2 \\ 3 \\ 0 \end{array}) = (\begin{array}{c} - 2 \\ 3 \\ - 1 \end{array})$
Der Punkt $P$ hat die Koordinaten $P (- 2 | 3 | - 1)$ .
Lösung zu c)
Für ein beliebiges Dreieck gilt die folgende Flächenformel: $A = \frac{1}{2} \cdot \sqrt{{\vec{a}}^{2} \cdot {\vec{b}}^{2} - (\vec{a} \circ \vec{b})^{2}}$
$\vec{a} = \vec{B C} = (\begin{array}{c} - 4 \\ 0 \\ - 1 \end{array}) - (\begin{array}{c} - 5 \\ 3 \\ 1 \end{array}) = (\begin{array}{c} 1 \\ - 3 \\ - 2 \end{array})$
$\vec{b} = \vec{A C} = (\begin{array}{c} - 4 \\ 0 \\ - 1 \end{array}) - (\begin{array}{c} - 7 \\ 0 \\ 1 \end{array}) = (\begin{array}{c} 3 \\ 0 \\ - 2 \end{array})$
Eingesetzt in die Flächenformel:
$A = \frac{1}{2} \cdot \sqrt{{(\begin{array}{c} 1 \\ - 3 \\ - 2 \end{array})}^{2} \cdot {(\begin{array}{c} 3 \\ 0 \\ - 2 \end{array})}^{2} - {((\begin{array}{c} 1 \\ - 3 \\ - 2 \end{array}) \circ (\begin{array}{c} 3 \\ 0 \\ - 2 \end{array}))}^{2}}$
$A = \frac{1}{2} \cdot \sqrt{(1 + 9 + 4) \cdot (9 + 0 + 4) - (3 + 0 + 4)^{2}}$
$A = \frac{1}{2} \cdot \sqrt{14 \cdot 13 - 7^{2}} = \frac{1}{2} \cdot \sqrt{133}$
Antwort: Das Dreieck $A B C$ hat einen Flächeninhalt von $\frac{1}{2} \cdot \sqrt{133} FE$ .
Aufgabe 9.1
1. Wähle einen beliebigen Punkt $P_{1} \in E_{1}$ .
2. Wähle einen beliebigen Punkt $P_{2} \in E_{2}$ .
3. Berechne den Mittelpunkt $M$ der Strecke $[P_{1} P_{2}]$ .
$\vec{O M} = \frac{1}{2} \cdot (\vec{O P_{1}} + \vec{O P_{2}})$
4. Nimm von den Ebenen $E_{1}$ oder $E_{2}$ einen der beiden Normalenvektoren z.B. ${\vec{n}}_{E_{1}}$ .
5. Setze in die Normalenform ein:
$F : (\vec{x} - \vec{O M}) \circ {\vec{n}}_{E_{1}} = 0$ .
Aufgabe 9.2
Gegeben $E : a x_{1} + b x_{2} + c x_{3} - d = 0$
$\Rightarrow \vec{n_{E}} = (\begin{array}{c} a \\ b \\ c \end{array})$
Der dazugehörende Normaleneinheitsvektor ist dann:
$\vec{n_{E}^{0}} = \frac{1}{\sqrt{a^{2} + b^{2} + c^{2}}} \cdot (\begin{array}{c} a \\ b \\ c \end{array})$
Finde einen Punkt $Q \in E$ . Dann führt die Vektorgleichung $\vec{O P} = \vec{O Q} + 3 \cdot \vec{n_{E}^{0}}$ zu einem Punkt $P \in F$ .
Da $F ∥ E$ ist $\vec{n_{F}} = \vec{n_{E}}$ . Mit dem Punkt $P$ kann die Gleichung der Ebene $F$ in Normalenform angegeben werden.
$F : (\vec{x} - \vec{O P}) \circ {\vec{n}}_{E} = 0$
Aufgabe 9.3
Erstelle eine Parameterform der Ebene $E$ , in der das Parallelogramm liegt.
z.B. $E : \vec{x} = \vec{O A} + r \cdot \vec{A B} + s \cdot \vec{A D}$
Prüfe, ob $P \in E$ ?
$(I) \vec{O P} = \vec{O A} + r \cdot \vec{A B} + s \cdot \vec{A D}$
1. Gleichung $(I)$ hat keine Lösung, dann gilt $P \notin E$ und $P \notin □$ .
2. Gleichung $(I)$ hat eine Lösung, dann gilt $P \in E$ und $P \in □$ , wenn die Bedingung $0 \leq r, s \leq 1$ erfüllt ist.
Aufgabe 9.4
Lösung zu a)
Das Schaubild der Funktion kann z.B. so wie in der Abbildung aussehen.
Es hat folgende Eigenschaften:
$f (x) > 0$ (alle Funktionswerte liegen oberhalb der $x$ -Achse)
$f^{'} (x) > 0$ (die Steigung ist immer positiv)
$f^{''} (x) < 0$ (Der Graph ist rechtsgekrümmt)
Lösung zu b)
Es gilt: $f^{''} (x) < 0 \Leftrightarrow (f^{'} (x))^{'} < 0 \Rightarrow f^{'} (x)$ ist streng monoton fallend. Fällt die Steigung eines Funktionsgraphen permanent, dann ist der Graph rechtsgekrümmt.
Aufgabe 9.4
Ein Bernoulli-Experiment wird $15$ -mal durchgeführt ( $n = 15$ ). Dabei ist die Erfolgswahrscheinlichkeit $p = 0,6$ und $q = 1 - p = 0,4$ .
Ereignis $A$ : Es gibt höchstens $12$ Erfolge bei $15$ Wiederholungen.
(alternative Formulierung: Es gibt weniger als $13$ Erfolge bei $15$ Wiederholungen)

Rotationskörper	Axialschnitt
Zylinder	Rechteck
Kegel	gleichschenkliges Dreieck
Kugel	Kreis
Halbkugel	Halbkreis
Kegelstumpf	gleichschenkliges Trapez

x	$f_{- 3} (x)$	besonderer Punkt
-0,5	-3,24
0	-1	$S_{y}$
0,33	-0,88	HP
1	-0,95
3	-1

x	$f_{1} (x)$	besonderer Punkt
-3	2,85
-2	2,73
-1	2,63	TP
0	3	$S_{y}$
0,5	3,82
1	5,72

Testlösungen Abitur BW (2)

Aufgabe 8.1

Berechne den Erwartungswert:

$E (X) = x_{1} \cdot P (X = x_{1} ) + x_{2} \cdot P (X = x_{2} ) + \dots + x_{n} \cdot P (X = x_{n})$

$E (X) = 30000 \cdot \frac{10}{10000} + 10000 \cdot \frac{50}{10000} + 2000 \cdot \frac{250}{10000} = 30 + 50 + 50 = 130$

Der Jahresbeitrag pro Kunde berechnet sich als Summe der mittleren Schadensfälle $E (X)$ und dem zu erwirtschafteten Gewinn $G = 100 €$ .

Jahresbeitag $= 130 € + 100 € = 230 €$

Antwort: Pro Versicherungskunde muss ein Jahresbeitrag von $230 €$ verlangt werden.

Aufgabe 8.2

Lösung zu a)

Treffer= $T$ ; kein Treffer (Niete)= $N$ ; $P (T) = 0,8$ und $P (N) = 1 - P (T) = 1 - 0,8 = 0,2$

Er trifft nur mit dem ersten Schuss: $P (T N N) = 0,8 \cdot 0,2 \cdot 0,2 = 0,032$

Mindestens $1$ Schuss trifft:

$P (mindestens 1 Treffer) = 1 - P (kein Treffer) = 1 - {0,2}^{3} = 1 - 0,008 = 0,992$

Antwort: Die Wahrscheinlichkeit nur mit dem $1.$ Schuss zu treffen beträgt $0,032$ und die Wahrscheinlichkeit, dass mindestens $1$ Schuss trifft, beträgt $0,992$ .

Lösung zu b)

Willst du die Wahrscheinlichkeit von $k$ Treffern eines Ereignisses mit der Wahrscheinlichkeit $p$ in einer Bernoulli-Kette der Länge $n$ berechnen, dann benutzt du den Binomialkoeffizienten: $B (n, p, k) = (\binom{n}{k}) \cdot p^{k} \cdot (1 - p)^{n - k}$

Vergleichst du die gegebene Wahrscheinlichkeit $P (A) = (\binom{10}{a}) \cdot b^{7} \cdot {0,2}^{c}$ für das Ereignis $A$ mit dem Binomialkoeffizienten $B (n, p, k)$ , dann ist $n = 10$ , $a = k = 7$ und $b = p = 0,8$ .

Antwort: Das Ereignis $A$ lautet demnach: Bei $10$ Schussversuchen werden genau $7$ Treffer erzielt.

Aufgabe 8.3

Lösung zu a)

Wird keine $6$ gewürfelt, verliert der Spieler seinen Einsatz $1$ $ $\Rightarrow x_{1} = - 1$

Wird eine $6$ gewürfelt, gewinnt der Spieler seinen Einsatz $1$ $ $\Rightarrow x_{2} = 0$

Werden zwei $6$ er gewürfelt, gewinnt der Spieler $1$ $ $\Rightarrow x_{3} = 1$

Werden drei $6$ er gewürfelt, gewinnt der Spieler $2$ $ $\Rightarrow x_{4} = 2$

Die dazugehörigen Wahrscheinlichkeiten sind in der Tabelle angegeben.

Zufallsvariable $x_{i}$	-1	0	1	2
$P (X = x_{i})$	${(\frac{5}{6})}^{3} = \frac{125}{216}$	$(\binom{3}{1}) \cdot \frac{1}{6} \cdot {(\frac{5}{6})}^{2} = \frac{75}{216}$	$(\binom{3}{2}) \cdot {(\frac{1}{6})}^{2} \cdot {(\frac{5}{6})}^{1} = \frac{15}{216}$	${(\frac{1}{6})}^{3} = \frac{1}{216}$

Lösung zu b)

Berechne den Erwartungswert:

$E (X) = x_{1} \cdot P (X = x_{1} ) + x_{2} \cdot P (X = x_{2} ) + \dots + x_{n} \cdot P (X = x_{n})$

$E (X) = (- 1) \cdot \frac{125}{216} + 0 \cdot \frac{75}{216} + 1 \cdot \frac{15}{216} + 2 \cdot \frac{1}{216} = - \frac{108}{216} = - 0,5$

Antwort: Der Spieler verliert im Mittel $0,5$ $ pro Spiel. Es ist kein faires Spiel.

Aufgabe 8.4

Es werden zwei Karten umgedreht. Dabei soll gelten: $P (1 Herz) = \frac{8}{15}$

Erstelle ein Baumdiagramm.

Die Zahl der Herzkarten ist gleich $n .$

Dann gilt für die Wahrscheinlichkeit: $P (1 Herz) = P (K H) + P (H K) = \frac{8}{15}$

Aus dem Baumdiagramm können die Wahrscheinlichkeiten für die zwei Pfade $P (K H)$ und $P (H K$ ) abgelesen werden.

$\frac{4}{4 + n} \cdot \frac{n}{3 + n} + \frac{n}{4 + n} \cdot \frac{4}{3 + n}$	$=$	$\frac{8}{15}$
	↓	Addiere die Brüche.
$\frac{8 n}{(4 + n) \cdot (3 + n)}$	$=$	$\frac{8}{15}$	$\cdot \frac{15}{8}$
$\frac{15 n}{(4 + n) \cdot (3 + n)}$	$=$	$1$	$\cdot (4 + n) \cdot (3 + n)$
$15 n$	$=$	$(4 + n) \cdot (3 + n)$
	↓	Löse die Klammer auf.
$15 n$	$=$	$12 + 4 n + 3 n + n^{2}$	$- 15 n$
$0$	$=$	$n^{2} - 8 n + 12$

Du hast eine quadratische Gleichung erhalten. Diese kannst du nun mit der Mitternachtsformel (abc-Formel) oder pq-Formel lösen.

Hier erfolgt die Lösung mit der pq-Formel. Lies die Werte für $p$ und $q$ ab: $p = - 8$ und $q = 12$

$n_{1,2}$	$=$	$- \frac{p}{2} \pm \sqrt{{(\frac{p}{2})}^{2} - q}$
	↓	Setze $p = - 8$ und $q = 12$ ein.
	$=$	$- \frac{(- 8)}{2} \pm \sqrt{{(d \frac{- 8}{2})}^{2} - 12}$
	↓	Vereinfache
	$=$	$4 \pm \sqrt{16 - 12}$
	$=$	$4 \pm \sqrt{4}$
	$=$	$4 \pm 2$
$n_{1}$	$=$	$2$
$n_{2}$	$=$	$6$

Antwort: Befinden sich entweder $2$ oder $6$ Herzkarten im Stapel, so ist die Wahrscheinlichkeit, dass unter den zwei aufgedeckten Karten genau eine Herzkarte ist, gleich $\frac{8}{15}$ .

Aufgabe 8.5

Lösung zu a)

Ziehen mit Zurücklegen.

Weiße Kugel: $w$

Schwarze Kugel: $s$

$P (mindestens 1 w) = 1 - P (kein w) = 1 - P (s s) = 1 - {(\frac{3}{5})}^{2} = \frac{16}{25} = 0,64$

Antwort: Die Wahrscheinlichkeit, dass mindestens eine Kugel weiß ist, beträgt $64$ %.

Lösung zu b)

Es befinden sich $3$ schwarze und $n$ weiße Kugeln im Behälter.

Ziehen mit Zurücklegen.

$P (mindestens 1 w) = 1 - P (kein w) = 1 - P (s s) = 0,91 \Rightarrow P (s s) = 1 - 0,91 = 0,09$

$P (s s) = {(\frac{3}{n + 3})}^{2} = 0,09 \Rightarrow \frac{9}{(n + 3)^{2}} = 0,09 \Rightarrow 100 = (n + 3)^{2}$

$(n + 3)^{2}$	$=$	$100$	$\sqrt{}$
	↓	Löse nach $n$ auf.
$n + 3$	$=$	$\pm 10$	$- 3$
$n$	$=$	$\pm 10 - 3$
$n_{1}$	$=$	$- 13$
	↓	Die negative Lösung entfällt.
$n_{2}$	$=$	$7$

Antwort: Befinden sich $3$ schwarze und $7$ weiße Kugeln im Behälter, dann beträgt die Wahrscheinlichkeit mindestens eine weiße Kugel zu ziehen $0,91$ .

Aufgabe 8.6

Lösung zu a)

Der Erwartungswert bei einer Binomialverteilung ist $E (X) = n \cdot p = 8 \cdot 0,75 = 6$

Das Maximum der Verteilung muss also bei $6$ liegen. Es kommen nur die Abbildungen $1$ und $3$ infrage.

Die Abbildung $3$ entfällt, da $n = 8$ und hier die Versuchsanzahl $n = 10$ ist.

Antwort: Die Abbildung $1$ ist die gesuchte Abbildung.

Lösung zu b)

Es gilt: $P (3 < X < 6) = P (x = 4) + P (x = 5) \approx 0,08 + 0,21 = 0,29$

$P (X \neq 8) = 1 - P (X = 8) \approx 1 - 0,1 = 0,9$

Antwort: $P (3 < X < 6) = 0,29$ und $P (X \neq 8) = 0,9$ .

Aufgabe $A 1.1$

Lösung zu a)

Zum Schaubild $C_{1}$ gehört die Funktion $f_{1} (x) = \frac{1}{2} \cdot (e^{x} + e^{- x})$ .

Bei Achsensymmetrie zur $y$ -Achse gilt: $f_{1} (- x) = f_{1} (x)$

$\Rightarrow f_{1} (- x) = \frac{1}{2} \cdot (e^{- x} + e^{- (- x})) = \frac{1}{2} \cdot (e^{- x} + e^{x}) = f_{1} (x)$

Tiefpunkt von $C_{1}$ : $f_{1}^{'} (x) = 0$

$f_{1}^{'} (x) = \frac{1}{2} \cdot (e^{x} + e^{- x} \cdot (- 1)) = \frac{1}{2} \cdot (e^{x} - e^{- x})$

$f_{1}^{'} (x)$	$=$	$0$
$\frac{1}{2} \cdot (e^{x} - e^{- x})$	$=$	$0$	$\cdot 2$
$e^{x} - e^{- x}$	$=$	$0$	$\cdot e^{x}$
	↓	Beseitige den negativen Exponenten.
$e^{2 x} - 1$	$=$	$0$	$+ 1$
	↓	Löse nach $x$ auf.
$e^{2 x}$	$=$	$1$	$\ln$
$2 x$	$=$	$\ln (1)$
$2 x$	$=$	$0$	$: 2$
$x$	$=$	$0$

An der Stelle $x = 0$ liegt ein Extremum vor. Da im Aufgabentext von einem Tiefpunkt die Rede ist, muss die hinreichende Bedingung nicht überprüft werden.

Berechne $f (0)$ : $f (0) = \frac{1}{2} \cdot (e^{0} + e^{- 0}) = \frac{1}{2} \cdot 2 = 1$

Der Tiefpunkt hat die Koordinaten $T P (0 | 1)$ .

Lösung zu b)

$A_{k} = \int_{0}^{\frac{1}{k}} \frac{1}{2 k} \cdot (e^{k x} + e^{- k x}) d x$

$= \frac{1}{2 k} \cdot {[\frac{e^{k x}}{k} - \frac{e^{- k x}}{k}]}_{0}^{\frac{1}{k}}$

$= \frac{1}{2 k^{2}} \cdot {[e^{k x} - e^{- k x}]}_{0}^{\frac{1}{k}}$

$= \frac{1}{2 k^{2}} \cdot [(e^{1} - e^{- 1}) - (1 - 1)]$

$= \frac{1}{2 k^{2}} \cdot (e^{1} - e^{- 1})$

Der Inhalt der eingeschlossenen Fläche beträgt $A_{k} = \frac{1}{2 k^{2}} \cdot (e^{1} - e^{- 1})$ .

Lösung zu c)

Lege das Koordinatensystem symmetrisch zur Hängebrücke, d.h. die $x$ -Achse ist der Boden und die $y$ -Achse geht durch die Brückenmitte.

Gegeben ist die Funktion $g (x) = a \cdot \frac{e^{k x} + e^{- k x}}{2 k}$

Da die Hängebrücke für $x = 0$ eine Höhe von $5 m$ hat, gilt $g (0) = 5$

$\Rightarrow g (0) = a \cdot \frac{e^{k \cdot 0} + e^{- k \cdot 0}}{2 k} = a \cdot \frac{1 + 1}{2 k} = a \cdot \frac{2}{2 k} = \frac{a}{k} = 5$

Andererseits gilt $g (10) = 8$

$\Rightarrow \frac{}{} a \cdot \frac{e^{k \cdot 10} + e^{- k \cdot 10}}{2 k} = 8$

$\Rightarrow \frac{a}{k} \cdot \frac{e^{k \cdot 10} + e^{- k \cdot 10}}{2} = 8$

$\Rightarrow \frac{a}{k} \cdot (e^{k \cdot 10} + e^{- k \cdot 10}) = 16$

Mit $\frac{a}{k} = 5$ folgt dann: $5 \cdot (e^{k \cdot 10} + e^{- k \cdot 10}) = 16$ bzw. $e^{k \cdot 10} + e^{- k \cdot 10} = \frac{16}{5}$

$e^{k \cdot 10} + e^{- k \cdot 10}$	$=$	$\frac{16}{5}$	$\cdot e^{k \cdot 10}$
	↓	Beseitige den negativen Exponenten.
$e^{20 \cdot k} + 1$	$=$	$\frac{16}{5} \cdot e^{10 \cdot k}$	$- \frac{16}{5} \cdot e^{10 \cdot k}$
	↓	Bringe die Terme auf eine Seite.
$e^{20 \cdot k} - \frac{16}{5} \cdot e^{10 \cdot k} + 1$	$=$	$0$
	↓	Setze $z = e^{10 \cdot k}$ .
$z^{2} - \frac{16}{5} z + 1$	$=$	$0$

Du hast eine quadratische Gleichung erhalten. Diese kannst du nun mit der Mitternachtsformel (abc-Formel) oder mit der pq-Formel lösen. Hier erfolgt die Lösung mit der pq-Formel.

Lies dazu die Werte von p und q ab: $p = - \frac{16}{5}$ und $q = 1$

$z_{1,2}$	$=$	$- \frac{p}{2} \pm \sqrt{{(\frac{p}{2})}^{2} - q}$
	$=$	$- \frac{(- \frac{16}{5})}{2} \pm \sqrt{{(\frac{- \frac{16}{5}}{2})}^{2} - 1}$
	↓	Vereinfache.
	$=$	$\frac{8}{5} \pm \sqrt{{(\frac{8}{5})}^{2} - 1}$
	$=$	$\frac{8}{5} \pm \sqrt{\frac{64}{25} - 1}$
	$=$	$\frac{8}{5} \pm \sqrt{\frac{39}{25}}$
	$=$	$\frac{8 \pm \sqrt{39}}{5}$
$z_{1}$	$=$	$\frac{8 - \sqrt{39}}{5}$
$z_{1}$	$\approx$	$0,351$
$z_{2}$	$=$	$\frac{8 + \sqrt{39}}{5}$
$z_{2}$	$\approx$	$2,849$

Rücksubstitution ergibt: $0,351 = e^{10 k}$ $\Rightarrow k_{1} = 0,1 \cdot \ln (0,351) \approx - 0,105$

Die Lösung $k_{1} = - 0,105$ entfällt, da $k$ laut Aufgabenstellung $> 0$ sein soll.

Damit folgt aus der zweiten Lösung $2,849 = e^{10 k} \Rightarrow k = 0,1 \cdot \ln (2,849) \approx 0,105$

Mit der am Anfang ermittelten Beziehung $\frac{a}{k} = 5 \Rightarrow a = 5 \cdot k \Rightarrow a = 5 \cdot 0,105 = 0,525$

Antwort: Die gesuchten Parameter lauten $k = 0,105$ und $a = 0,525$ .

Lösung zu d)

Der Punkt $A$ hat die Koordinaten $A (10 | 8)$ .

Die Funktion $g (x)$ lautet: $g (x) = \frac{0,525}{2 \cdot 0,105} \cdot (e^{0,105 \cdot x} + e^{- 0,105 \cdot x}) = 2,5 \cdot (e^{0,105 \cdot x} + e^{- 0,105 \cdot x})$

Berechne die Ableitung, beachte dabei die Kettenregel: $g^{'} (x) = 2,5 \cdot 0,105 \cdot (e^{0,105 \cdot x} - e^{- 0,105 \cdot x})$

$g^{'} (x) = 0,2625 \cdot (e^{0,105 \cdot x} - e^{- 0,105 \cdot x})$

An der Stelle $x = 10$ erhältst du für die Ableitung:

$g^{'} (10) = 0,2625 \cdot (e^{0,105 \cdot 10} - e^{- 0,105 \cdot 10}) = 0,2625 \cdot (e^{1,05} - e^{- 1,05}) \approx 0,658$

Um den Winkel zu berechnen, setze $\tan (α) = g^{'} (10) = 0,658 \Rightarrow α \approx {33,3}^{\circ}$

Antwort: Die Brücke trifft unter einem Winkel von etwa ${33,3}^{\circ}$ im Punkt $A$ auf die waagrechte Plattform.

Lösung zu e)

Gesucht ist zunächst die Gleichung der Normalen vom Punkt $B (10 | 0)$ an den Graphen von $g (x)$ .

Allgemein lautet die Normalengleichung im Punkt $P (x_{0} | g (x_{0})$ :

$n (x) = - \frac{1}{g^{'} (x_{0})} \cdot (x - x_{0}) + g (x_{0})$

Setze $g^{'} (x_{0})$ in $n (x)$ ein $\Rightarrow n (x) = - \frac{1}{0,2625 \cdot (e^{0,105 \cdot x_{0}} - e^{- 0,105 \cdot x_{0}})} \cdot (x - x_{0}) + g (x_{0})$

$\Rightarrow n (x) = - \frac{1}{0,2625 \cdot (e^{0,105 \cdot x_{0}} - e^{- 0,105 \cdot x_{0}})} \cdot (x - x_{0}) + 2,5 \cdot (e^{0,105 \cdot x_{0}} + e^{- 0,105 \cdot x_{0}})$

Der Punkt $B (10 | 0)$ muss die Normalengleichung erfüllen. $B$ eingesetzt ergibt die folgende Gleichung:

$0 = - \frac{1}{0,2625 \cdot (e^{0,105 \cdot x_{0}} - e^{- 0,105 \cdot x_{0}})} \cdot (10 - x_{0}) + 2,5 \cdot (e^{0,105 \cdot x_{0}} + e^{- 0,105 \cdot x_{0}})$

Umgeformt erhältst du:

$10 - x_{0} = 2,5 \cdot (e^{0,105 \cdot x_{0}} + e^{- 0,105 \cdot x_{0}}) \cdot 0,2625 \cdot (e^{0,105 \cdot x_{0}} - e^{- 0,105 \cdot x_{0}})$

Beachte die $3$ . binomische Formel:

$10 - x_{0} = 0,65625 \cdot (e^{0,21 \cdot x_{0}} - e^{- 0,21 \cdot x_{0}})$

Die Gleichung kannst du mit der SOLVE - Funktion deines Taschenrechners lösen.

Du erhältst: $x_{0} \approx 7,18$

Eingesetz in $g (x)$ folgt: $g (7,18) = 2,5 \cdot (e^{0,105 \cdot 7,18} + e^{- 0,105 \cdot 7,18}) \approx 6,49$

Antwort: Der Befestigungspunkt $P$ hat die Koordinaten $P (7,18 | 6,49)$ .

Aufgabe $A 1.2$

Lösung

Die Funktion $k (x)$ ist eine Ursprungsgerade mit der Steigung $m = \frac{r}{h}$ .

Damit gilt: $k (x) = \frac{r}{h} \cdot x$

Das Rotationsvolumen berechnest du mit der Formel

$V = π \cdot \int_{0}^{h} {(k (x))}^{2} d x \Rightarrow$

$V = π \cdot \int_{0}^{h} {(\frac{r}{h} \cdot x)}^{2} d x \Rightarrow$

$V = \frac{π \cdot r^{2}}{h^{2}} \cdot \int_{0}^{h} x^{2} d x = \frac{π \cdot r^{2}}{h^{2}} \cdot {[\frac{1}{3} x^{3}]}_{0}^{h} \Rightarrow$

$V = \frac{π \cdot r^{2}}{h^{2}} \cdot (\frac{1}{3} h^{3} - 0) = \frac{1}{3} π \cdot r^{2} \cdot h$

Antwort: Für das Kegelvolumen gilt die Formel $V_{K} = \frac{1}{3} π \cdot r^{2} \cdot h$

Aufgabe $B 1$

Lösung zu a)

Die Ebene $E_{1}$ hat die Gleichung $E_{1} : x_{1} + x_{2} = 2 \Rightarrow \frac{x_{1}}{2} + \frac{x_{2}}{2} = 1$

Aus der Achsenabschnittsform können die Achsenschnittpunkte (Spurpunkte) abgelesen werden:

$S_{x_{1}} (2 | 0 | 0)$ (Punkt $A$ in der Zeichnung) und $S_{x_{2}} (0 | 2 | 0)$ (Punkt $P$ in der Zeichnung)

Es gibt keinen Schnittpunkt mit der $x_{3}$ -Achse, d. h. die Ebene $E_{1}$ verläuft parallel zur $x_{3}$ -Achse.

Nachweis, dass der Spiegel in der Ebene $E_{1}$ liegt

Prüfe, ob die vier Punkte des Spiegels in der Ebene $E_{1}$ liegen:

$A = S_{x_{1}}$ , damit ist $A \in E_{1}$

$B (- 2 | 4 | 0) \in E_{1} ? \Rightarrow - 2 + 4 = 2 ✓$

$C (- 2 | 4 | 4) \in E_{1} ? \Rightarrow - 2 + 4 = 2 ✓$

$D (2 | 0 | 4) \in E_{1} ? \Rightarrow 2 + 0 = 2 ✓$

Damit liegt der Spiegel in der Ebene $E_{1}$ .

Die Ebene $E_{3}$ hat die Gleichung $E_{3} : x_{1} + 3 \cdot x_{2} = 6 \Rightarrow \frac{x_{1}}{6} + \frac{x_{2}}{2} = 1$

Aus der Achsenabschnittsform können die Achsenschnittpunkte abgelesen werden:

$S_{x_{1}} (6 | 0 | 0)$ und $S_{x_{2}} (0 | 2 | 0)$ (Punkt $P$ in der Zeichnung)

Es gibt keinen Schnittpunkt mit der $x_{3}$ -Achse, d. h. die Ebene $E_{3}$ verläuft parallel zur $x_{3}$ -Achse.

Darstellung des Spiegels $A B C D$ in der Ebene $E_{1}$ (orange). Gedrehter Spiegel in der Ebene $E_{3}$ (grün). Drehachse [PQ].

Spiegeldrehung

Drehung des Spiegels um den Winkel $α$ , um die Achse $[P Q]$ . Der Winkel $α$ ist der Winkel zwischen den beiden Ebenen $E_{1}$ und $E_{3}$ .

Aus den Koordinatendarstellungen der beiden Ebenen kannst du die Normalenvektoren ablesen:

${\vec{n}}_{E_{1}} = (\begin{array}{c} 1 \\ 1 \\ 0 \end{array})$ und ${\vec{n}}_{E_{3}} = (\begin{array}{c} 1 \\ 3 \\ 0 \end{array})$

Damit gilt für den Winkel: $\cos α = \frac{{\vec{n}}_{E_{1}} \circ {\vec{n}}_{E_{3}}}{| {\vec{n}}_{E_{1}} | \cdot | {\vec{n}}_{E_{3}} |}$

$\Rightarrow \cos α = \frac{(\begin{array}{c} 1 \\ 1 \\ 0 \end{array}) \circ (\begin{array}{c} 1 \\ 3 \\ 0 \end{array})}{| (\begin{array}{c} 1 \\ 1 \\ 0 \end{array}) | \cdot | (\begin{array}{c} 1 \\ 3 \\ 0 \end{array}) |} = \frac{1 + 3 + 0}{\sqrt{1^{2} + 1^{2} + 0^{2}} \cdot \sqrt{1^{2} + 3^{2} + 0^{2}}} = \frac{4}{\sqrt{2} \cdot \sqrt{10}} = \frac{4}{\sqrt{20}}$

$α = \arccos (\frac{4}{\sqrt{20}}) \approx {26,57}^{\circ}$

Antwort: Der Spiegel wurde um etwa ${26,57}^{\circ}$ gedreht.

Lage der Ebene $E_{t}$ in Abhängigkeit von $t$

$E_{t} : x_{1} + t \cdot x_{2} = 2 \cdot t$

Es gibt keinen Schnittpunkt mit der $x_{3}$ -Achse, d. h. die Ebene $E_{t}$ verläuft parallel zur $x_{3}$ -Achse.

Für $t = 0$ ist $x_{1} = 0$ , d.h. die Ebene $E_{0}$ liegt in der $x_{2} x_{3}$ -Ebene. Wenn der Betrag von $t$ größer wird, wird die $x_{1}$ -Achse bei größeren $x_{1}$ -Werten geschnitten $(S_{x_{1}} (2 t | 0 | 0))$ , während der Schnittpunkt mit der $x_{2}$ -Achse gleich bleibt $(S_{x_{2}} (0 | 2 | 0))$ . Die Ebene (und damit auch der Spiegel) dreht sich weiter um die Drehachse $[P Q]$ .

Liegt die Ebene (und damit auch der Spiegel) parallel zur $x_{1} x_{3}$ -Ebene, dann lautet die Ebenengleichung $x_{2} = 2$ . Für kein $t$ kann aber die Ebene $E_{t}$ die Gleichung $x_{2} = 2$ annehmen.

Lösung zu b)

$E_{3} : x_{1} + 3 \cdot x_{2} = 6$

Dargestellt ist die Spiegellage in der $x_{1} x_{2}$ -Ebene.

Gesucht sind die Spiegelkoordinaten $A^{'} B^{'} C^{'} D^{'}$ in der Ebene $E_{3}$ .

Der Spiegel ist $4$ Einheiten hoch und $| \vec{A B} |$ breit.

$\vec{A B} = (\begin{array}{c} - 2 \\ 4 \\ 0 \end{array}) - (\begin{array}{c} 2 \\ 0 \\ 0 \end{array}) = (\begin{array}{c} - 4 \\ 4 \\ 0 \end{array})$

$| \vec{A B} | = \sqrt{(- 4)^{2} + 4^{2} + 0^{2}} = \sqrt{32} = 2 \cdot \sqrt{8}$

Demnach ist $| \vec{P A^{'}} | = \frac{1}{2} \cdot | \vec{A B} | = \sqrt{8}$ und mit dem Satz des Pythagoras findest du:

$| P S_{x_{1}} | = \sqrt{6^{2} + 2^{2}} = \sqrt{40}$

Der Punkt $A^{'}$ hat die Koordinaten $A^{'} (a | b | 0)$ .

Im Dreieck $S_{x_{1}} O P$ kann dann der Strahlensatz angewendet werden.

$\frac{b}{2} = \frac{\sqrt{40} - \sqrt{8}}{\sqrt{40}} \Rightarrow b = 2 \cdot ((1 - \frac{1}{\sqrt{5}}) \approx 1,11$

Weiterhin gilt: $\frac{a}{6} = \frac{\sqrt{8}}{\sqrt{40}} \Rightarrow a = \frac{6}{\sqrt{5}} \approx 2,68$

Der Punkt $A^{'}$ hat die Koordinaten $A^{'} (2,68 | 1,11 | 0)$ .

Durch Symmetrieüberlegungen findest du die anderen Koordinaten des gedrehten Spiegels.

Die $x_{1}$ -Koordinate vom Punkt $B^{'}$ ist die negative $x_{1}$ -Koordinate des Punktes $A^{'}$ .

Die $x_{2}$ -Koordinate von $A^{'}$ ist $1,11$ . Aus der Zeichnung kannst du entnehmen, dass die $x_{2}$ -Koordinate vom Punkt $B^{'}$ gleich $2 + (2 - 1,11) = 2,89$ ist.

Der Punkt $B^{'}$ hat die Koordinaten $B^{'} (- 2,68 | 2,89 | 0)$ .

Der Punkt $C^{'}$ liegt $4$ Einheiten oberhalb des Punktes $B^{'}$ . Somit hat $C^{'}$ die Koordinaten $C^{'} (- 2,68 | 2,89 | 4)$ .

Der Punkt $D^{'}$ liegt $4$ Einheiten oberhalb des Punktes $A^{'}$ . Somit hat $D^{'}$ die Koordinaten $D^{'} (2,68 | 1,11 | 4)$ .

Antwort: $A^{'} (2,68 | 1,11 | 0); B^{'} (- 2,68 | 2,89 | 0); C^{'} (- 2,68 | 2,89 | 4); D^{'} (2,68 | 1,11 | 4)$

Lösung zu c)

Geradengleichung für den Lichtstrahl

$g_{L i c h t} : \vec{x} = (\begin{array}{c} 6 \\ 8 \\ 1 \end{array}) + r \cdot (\begin{array}{c} - 3 \\ - 3 \\ 1 \end{array})$

Berechne den Schnittpunkt der Geraden $g_{L i c h t}$ mit der Ebene $E_{t}$ :

$(6 - 3 r) + t \cdot (8 - 3 r)$	$=$	$2 t$
	↓	Löse die Klammern auf.
$6 - 3 r + 8 t - 3 r t$	$=$	$2 t$	$- 6 - 8 t$
	↓	Sortiere die Terme.
$- 3 r - 3 r t$	$=$	$- 6 - 6 t$	$\cdot (- 1)$
$3 r + 3 r t$	$=$	$6 + 6 t$
	↓	Klammere $r$ aus.
$r (3 + 3 t)$	$=$	$6 + 6 t$

Fallunterscheidung:

Fall 1: $t \neq - 1$

Die letzte Gleichung kann nach r aufgelöst werden.

$r (3 + 3 t)$	$=$	$6 + 6 t$	$: (3 + 3 t)$
$r$	$=$	$\frac{6 + 6 t}{3 + 3 t}$
	↓	Klammere im Zähler $2$ aus.
$r$	$=$	$\frac{2 (3 + 3 t)}{3 + 3 t}$
	↓	Kürze.
$r$	$=$	$2$

Fall 2: $t = - 1$

Setzt du $t = - 1$ in die Gleichung $r (3 + 3 t) = 6 + 6 t$ ein, dann erhältst du eine wahre Aussage $0 = 0$ , d.h. die Gerade liegt für $t = - 1$ in der Ebene $E_{t}$ .

Zur Berechnung des Schnittpunktes setze $r = 2$ in $g_{L i c h t}$ ein:

${\vec{x}}_{S} = (\begin{array}{c} 6 \\ 8 \\ 1 \end{array}) + 2 \cdot (\begin{array}{c} - 3 \\ - 3 \\ 1 \end{array}) = (\begin{array}{c} 0 \\ 2 \\ 3 \end{array})$

Der Schnittpunkt $S$ ist unabhängig von $t$ , d.h. der Spiegel wird immer im gleichen Punkt $S$ getroffen.

Der Punkt $S (0 | 2 | 3)$ liegt auf der Drehachse [PQ] des Spiegels.

Aufgabe $C 1$

Lösung zu a)

$A : P (X = 6) = (\binom{10}{6}) \cdot {0,6}^{6} \cdot (1 - 0,6)^{10 - 6} = (\binom{10}{6}) \cdot {0,6}^{6} \cdot {0,4}^{4} \approx 0,2508$

$B : P (X \geq 6) = 1 - P (x \leq 5) = 1 - F (10; 0,6; 5) = 1 - 0,3669 = 0,6331$

$C : p = {0,4}^{3} \cdot {0,6}^{7} \approx 0,0018$

Lösung zu b)

$P (X \geq 50) = 1 - P (x \leq 49) \geq 0,95 \Rightarrow F (100; p; 49) \leq 0,05$

Mithilfe des TR erhältst du $p \approx 0,577$ .

Lösung zu c)

Intervallbestimmung

$p_{\ddot{U} b e r g e w i c h t} = 0,54$ ; $n = 500$

Die Zufallsvariable $X$ ist $B_{500; 0,54}$ verteilt.

Den Mittelwert berechnest du mit $μ = n \cdot p = 500 \cdot 0,54 = 270$

Die Standardabweichung berechnest du mit $σ = \sqrt{n \cdot p \cdot (1 - p)} = \sqrt{500 \cdot 0,54 \cdot 0,46} \approx 11,14$

Für ein Intervall mit $95$ %-iger Wahrscheinlichkeit gilt: $[μ - 1,96 σ; μ + 1,96 σ]$

$\Rightarrow [270 - 1,96 \cdot 11,14; μ + 1,96 \cdot 11,14] = [270 - 21,83; 270 + 21,83] = [248,17; 291,83]$

Antwort: Die Anzahl der Übergewichtigen in dem Dorf liegt mit $95$ %-iger Wahrscheinlichkeit zwischen $248$ und $292$ Personen.

Hypothesentest

Gegeben sind $H_{0} : p \geq 0,54$ , $n = 90$ und das Signifikanzniveau $α = 10$ %

Es handelt sich um einen linksseitigen Test:

$α -Fehler : P (X \leq k) \leq 0,1$

$\Rightarrow F (90; 0,54; k) \leq 0,1$

Mit dem TR findest du:

$F (90; 0,54; 43) \approx 0,1404 \geq 0,1 und F (90; 0,54; 42) \approx 0,0986 \leq 0,1$

Also gilt $k = 42$ .

Antwort: Haben höchstens $42$ Mitglieder im Sportverein einen BMI $> 25$ , dann wird $H_{0}$ verworfen. Haben mehr als $42$ Mitglieder im Sportverein einen BMI $> 25$ , dann wird $H_{0}$ beibehalten.

9
Spiegelung von 2 parallelen Ebenen

Gegeben sind zwei (echt) parallele Ebenen in Koordinatenform:
$E : a_{1} \cdot x_{1} + b_{1} \cdot x_{2} + c_{1} \cdot x_{3} = d_{1}$ und $H : a_{1} \cdot x_{1} + b_{1} \cdot x_{2} + c_{1} \cdot x_{3} = d_{2}$ .
Die Ebene $E$ wird an der Ebene $H$ gespiegelt $\Rightarrow E^{'} : a_{1} \cdot x_{1} + b_{1} \cdot x_{2} + c_{1} \cdot x_{3} = d_{3}$
Wie wird $d_{3}$ berechnet?
Setzt man den Koordinatenursprung in die Hessesche Normalenform der Ebene ein, so erhält man den Abstand der Ebene vom Ursprung.
$E_{H N F} : \frac{a_{1} x_{1} + b_{1} x_{2} + c_{1} x_{3} - d_{1}}{| {\vec{n}}_{E} |} = 0$
$d (O, E) = | \frac{a_{1} \cdot 0 + b_{1} \cdot 0 + c_{1} \cdot 0 - d_{1}}{| {\vec{n}}_{E} |} | = \frac{d_{1}}{| {\vec{n}}_{E} |}$
Entsprechend für die Ebene $H$ :
$d (O, H) = | \frac{a_{1} \cdot 0 + b_{1} \cdot 0 + c_{1} \cdot 0 - d_{2}}{| {\vec{n}}_{H} |} | = \frac{d_{2}}{| {\vec{n}}_{H} |}$
Für den Abstand der Spiegelebene $E^{'}$ vom Koordinatenursprung gilt:
$d (O, E^{'}) = d (O, H) + d (E, H) = d (O, H) + (d (O H) - d (O, E)) = 2 \cdot d (O, H) - d (O, E)$
Da $| {\vec{n}}_{E} | = | {\vec{n}}_{H} | = | {\vec{n}}_{E}^{'} |$ gilt: $d (O, E^{'}) = \frac{d_{3}}{| {\vec{n}}_{E} |} = 2 \cdot \frac{d_{2}}{| {\vec{n}}_{E} |} - \frac{d_{1}}{| {\vec{n}}_{E} |}$
Für $d_{3}$ der Spiegelebene $E^{'}$ ergibt sich somit die Gleichung: $d_{3} = 2 \cdot d_{2} - d_{1}$
Satz
Die rechte Seite $d_{3}$ der Koordinatenform der Spiegelebene $E^{'}$ berechnet sich mit:
$d_{3} = 2 \cdot d_{2} - d_{1}$
Beispiel zu Fall 1
Gegeben sind die beiden (echt) parallelen Ebenen
$E : 5 \cdot x_{1} - x_{2} + 2 \cdot x_{3} = - 3$ und $H : 5 \cdot x_{1} - x_{2} + 2 \cdot x_{3} = - 30$ .
Die Ebene $E$ wird an der Ebene $H$ gespiegelt.
$d_{3} = 2 \cdot d_{2} - d_{1}$
Setze $d_{1} = - 3$ und $d_{2} = - 30$ ein:
$d_{3} = 2 \cdot (- 30) - (- 3) = - 60 + 3 = - 57$
Antwort: Die Gleichung der Spiegelebene $E^{'}$ lautet: $5 \cdot x_{1} - x_{2} + 2 \cdot x_{3} = - 57$
Alternative Berechnung der Spiegelung eines Punktes $P$ an einer Ebene $E$
Die Ebene ist durch $\vec{x} \circ \vec{n} = d$ gegeben.
Setze den gegebenen Punkt $P$ in die Ebenengleichung $E$ ein und berechne die Zahl $d_{1}$ :
$\Rightarrow (I) \vec{p} \circ \vec{n} = d_{1}$
Der Spiegelpunkt $P^{'}$ liegt dann in der Ebene $\vec{x} \circ \vec{n} = 2 \cdot d - d_{1}$ (siehe Spiegelung Ebene an Ebene)
$\Rightarrow (I I) \vec{p}^{'} \circ \vec{n} = 2 \cdot d - d_{1}$
Die Verbindung der Punkte $P$ und $P^{'}$ steht senkrecht auf der Ebene $E$ .
Damit ist $(I I I) \vec{p}^{'} = \vec{p} + t \cdot \vec{n}$ .
Zur Berechnung des Spiegelpunktes muss also der Parameter $t$ berechnet werden:
Setze $(I I I)$ in $(I I)$ ein:
$\vec{p}^{'} \circ \vec{n}$ $=$ $2 \cdot d - d_{1}$
↓
Setze $\vec{p}^{'} = \vec{p} + t \cdot \vec{n}$ ein.
$(\vec{p} + t \cdot \vec{n}) \circ \vec{n}$ $=$ $2 \cdot d - d_{1}$
$\vec{p} \circ \vec{n} + t \cdot \vec{n} \circ \vec{n}$ $=$ $= 2 \cdot d - d_{1}$
Die Gleichung $(I V)$ lautet: $\vec{p} \circ \vec{n} + t \cdot \vec{n} \circ \vec{n} = 2 \cdot d - d_{1}$
Setze $(I)$ in $(I V)$ ein:
$\vec{p} \circ \vec{n} + t \cdot \vec{n} \circ \vec{n}$ $=$ $2 \cdot d - d_{1}$
↓
Setze $\vec{p} \circ \vec{n} = d_{1}$ ein.
$d_{1} + t \cdot \vec{n} \circ \vec{n}$ $=$ $2 \cdot d - d_{1}$ $- d_{1}$
$t \cdot \vec{n} \circ \vec{n}$ $=$ $2 \cdot d - 2 \cdot d_{1}$
$t \cdot \vec{n} \circ \vec{n}$ $=$ $2 \cdot (d - d_{1})$ $: \vec{n} \circ \vec{n}$
$t$ $=$ $\frac{2 \cdot (d - d_{1})}{\vec{n} \circ \vec{n}}$
Mit diesem Parameter $t$ kann nun der Spiegelpunkt $P^{'}$ berechnet werden:
$\vec{p}^{'} = \vec{p} + t \cdot \vec{n} $
Beispiel
Gegeben sind der Punkt $P (3 | 2 | 1)$ und die Ebene $E : \vec{x} \circ (\begin{array}{c} 1 \\ 0 \\ - 1 \end{array}) = 6$ . Spiegele den Punkt $P$ an der Ebene $E$ .
Lösung
Gegeben sind der zu spiegelnde Punkt $P (3 | 2 | 1)$ , der Normalenvektor $\vec{n}$ der Ebene $E$
$\vec{n} = (\begin{array}{c} 1 \\ 0 \\ - 1 \end{array})$ und $d = 6$ .
1. Setze den gegebenen Punkt $P$ in die Ebenengleichung $E : \vec{x} \circ (\begin{array}{c} 1 \\ 0 \\ - 1 \end{array}) = 6$ ein und berechne die Zahl $d_{1}$ :
$(\begin{array}{c} 3 \\ 2 \\ 1 \end{array}) \circ (\begin{array}{c} 1 \\ 0 \\ - 1 \end{array}) = d_{1} \Rightarrow d_{1} = 3 \cdot 1 + 2 \cdot 0 + 1 \cdot (- 1) = 3 + 0 - 1 = 2$
2. Berechne $\vec{n} \circ \vec{n}$ :
$(\begin{array}{c} 1 \\ 0 \\ - 1 \end{array}) \circ (\begin{array}{c} 1 \\ 0 \\ - 1 \end{array}) = 1 \cdot 1 + 0 \cdot 0 + (- 1) \cdot (- 1) = 1 + 0 + 1 = 2$
3. Berechne den Parameter $t$ mit $d = 6$ , $d_{1} = 2$ und $\vec{n} \circ \vec{n} = 2$ :
$t = \frac{2 \cdot (d - d_{1})}{\vec{n} \circ \vec{n}} = \frac{2 \cdot (6 - 2)}{2} = 4$
4. Berechne $\vec{p}^{'}$ :
$\vec{p}^{'} = \vec{p} + t \cdot \vec{n} = (\begin{array}{c} 3 \\ 2 \\ 1 \end{array}) + 4 \cdot (\begin{array}{c} 1 \\ 0 \\ - 1 \end{array}) = (\begin{array}{c} 3 + 4 \\ 2 + 0 \\ 1 - 4 \end{array}) = (\begin{array}{c} 7 \\ 2 \\ - 3 \end{array})$
Antwort: Der Spiegelpunkt hat die Koordinaten $P^{'} (7 | 2 | - 3)$ .

Kowalskys Testaufgabe

$\cos (α) = \frac{\vec{a} \circ \vec{b}}{| \vec{a} | \cdot | \vec{b} |}$

Lösung von Gleichungen-Übersicht

a)
Berechnen Sie die Konzentration eine Stunde nach der Einnahme des Medikamentes.
Zeichne den Graphen von $f (x) = 5 \cdot (e^{- 0,3 x} - e^{- 4 x})$ .
Finde mit TRACE den y-Wert zu $x = 1 \Rightarrow y \approx 3,6$
Somit beträgt die Konzentration nach einer Stunde noch rund $3,6 \frac{mg}{l}$
Geben Sie den Zeitpunkt an, zu dem die Konzentration erstmals den Wert $2,8 \frac{mg}{l}$ annimmt.
Zeichne zu dem Graphen von $f (x)$ den Graphen von $y = 2,8$ .
Finde den ersten Schnittpunkt der beiden Graphen:
$\Rightarrow x_{1} \approx 0,25$
Dabei ist $x$ in Stunden angegeben.
$0,25$ Stunden sind $0,25 \cdot 60 = 15$ Minuten.
Also wird der Wert erstmals nach ca. 15 Minuten überschritten.
Bestimmen Sie, wie lange die Konzentration mindestens $0,5 \frac{mg}{l}$ beträgt.
Zeichne zu dem Graphen von $f (x)$ den Graphen von $y = 0,5$ .
Finde die Schnittpunkte der beiden Graphen:
$\Rightarrow x_{1} \approx 0,029$ und $x_{2} \approx 7,675$ (erneut in Stunden)
Um herauszufinden, wie lange die Konzentration im Blut mindestens $0,5 \frac{mg}{l}$ beträgt, subtrahierst du die beiden Zeitpunkte voneinander:
$Δ x = 7,68 - 0,03 = 7,65$ .
Da $f (x) > 0,5$ für $x_{1} < x < x_{2}$ gilt, ist die Konzentration ungefähr $7,6$ Stunden mindestens $0,5 \frac{mg}{l}$ groß.
b)
Die Gleichung $f^{'} (x) = 0$ hat für $0 \leq x \leq 12$ nur die Lösung $x_{H} \approx 0,7$ .
Betrachte für das Vorzeichenwechselkriterium Ableitungswerte in der Nähe von $x_{H}$ , z.B. ist $f^{'} (0,5) \approx 1,4 > 0$ und $f^{'} (0,9) \approx - 0,6$ . Es findet also ein VZW von $+ \mapsto -$ statt. Also liegt ein Hochpunkt vor.
e) Für $x \geq 6$ wird die Konzentration durch die Tangente $t$ an den Graphen von $f$
im Punkt $(6 | f (6))$ beschrieben:
$t (x) = m \cdot x + b$ mit $m \approx - 0,248$ und $b \approx 2,314$ .
Die Nullstelle der Tangente entspricht dem gesuchten Zeitpunkt in Stunden.
$𝑡$ hat die Nullstelle $x_{N}$ mit $x_{N} \approx 9,3$ .
Also sinkt die Konzentration 9,3 Stunden nach der Einnahme auf $0 \frac{mg}{l}$ .
g)
$f_{a}$ hat nur die Nullstelle $0$ .
Du suchst die Werte von $a,$ für die der Wert des Integrals gleich $0,2$ oder $- 0,2$ ist.
Fall 1
Dann ist $\int_{0}^{1} f (x) d x = F_{a} (1) - F_{a} (0) = 0,2$
Gegeben ist $F_{a} (x) = - \frac{1}{a} \cdot e^{- a \cdot x} + \frac{1}{4} e^{- 4 x}$ .
Dann ist $F_{a} (1) = - \frac{1}{a} \cdot e^{- a} + \frac{1}{4} e^{- 4}$ und $F_{a} (0) = - \frac{1}{a} + \frac{1}{4}$ .
Definiere die Funktionen $g (x) = - \frac{1}{x} \cdot e^{- x} + \frac{1}{4} e^{- 4}$ und $h (x) = \frac{1}{4} e^{- 4}$ .
Es gilt dann: $\int_{0}^{1} f (x) d x = g (x) - h (x) = 0,2$ oder $g (x) = h (x) + 0,2 = - \frac{1}{x} + 0,45$
Bestimme die Schnittstelle von $g (x)$ mit $- \frac{1}{x} + 0,45$ .
Du erhältst $x_{1} \approx 1,91$ , d.h. $a_{1} \approx 1,9$ .
Fall 2
Nun gilt: $\int_{0}^{1} f (x) d x = g (x) - h (x) = - 0,2$ .
Verfahre wie im Fall 1:
Nun gilt $g (x) = h (x) - 0,2 = - \frac{1}{x} + 0,05$ .
Bestimme die Schnittstelle von $g (x)$ mit $- \frac{1}{x} + 0,05$ .
Du erhältst $x_{2} \approx 22,016$ , d.h. $a_{2} \approx 22,0$ .
In einem Multiple-Choice-Test gibt es $20$ Aufgaben, bei denen man aus drei möglichen Lösungen die richtige ankreuzen muss. Felix hat sich nicht auf den Test vorbereitet. Mit welcher Wahrscheinlichkeit wird er trotzdem genau die Hälfte der Fragen richtig beantworten?
Berechne die Wahrscheinlichkeit, indem du die gegebenen Werte in die Formel der Binomialverteilung einsetzt:
$n = 20, p = \frac{1}{3}, k = 10$
Berechnet werden muss: $P (X = 10) = B (20, \frac{1}{3},10)$
Die Lösung erfolgt mit dem TR CASIO fx-991 DE PLUS:
Drücke die Taste MODE. Es erscheint folgende Auswahl:
Wähle 4: DIST
Wähle 4: Binomial PD
Wähle 2: Var
Gib hier den Wert $k = 10$ ein.
Gib hier den Wert $n = 20$ ein.
Gib hier den Wert $p = \frac{1}{3}$ ein.
Nach Druck der "="-Taste erscheint das Ergebnis:
p=0,054259....
Zu $5,4 %$ beantwortet er genau die Hälfte der Fragen richtig.

Gegeben ist der Kreis $k : x^{2} + y^{2} = 16$ . Durch den Punkt $P (- 8 | 0)$ verläuft eine Gerade $g$ , die Tangente an den Kreis sein soll. Berechne die Funktionsgleichung der Geraden und den Berührpunkt $B$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente

Tangentengleichung

Die allgemeine Geradengleichung lautet:

$g : y = m \cdot x + t$

Setze die Koordinaten des Punktes $P$ ein.

$y$	$=$	$m \cdot x + t$
	↓	Setze $P (- 8 \| 0)$ ein.
$0$	$=$	$m \cdot (- 8) + t$	$+ 8 m$
$8 m$	$=$	$t$

Damit lautet die Geradengleichung $g : y = m \cdot x + 8 m = m (x + 8)$

Zur Berechnung des Schnittpunktes zwischen der Geraden und dem Kreis setze $y$ in die Kreisgleichung ein.

$x^{2} + y^{2}$	$=$	$16$
	↓	Setze $y = m (x + 8)$ ein.
$x^{2} + (m (x + 8))^{2}$	$=$	$16$
$x^{2} + m^{2} x^{2} + 16 m^{2} x + 64 m^{2}$	$=$	$16$	$- 16$
$(1 + m^{2}) x^{2} + 16 m^{2} x + 64 m^{2} - 16$	$=$	$0$
$(1 + m^{2}) x^{2} + 16 m^{2} x + 16 (4 m^{2} - 1)$	$=$	$0$

Du hast eine quadratische Gleichung erhalten. Diese kannst du

nun mit der Mitternachtsformel (abc-Formel) lösen.

Lies die Werte für $a$ , $b$ und $c$ ab.

$a = (1 + m^{2})$ , $b = 16 m^{2}$ und $c = 16 (4 m^{2} - 1)$

$x_{1,2}$	$=$	$\frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$
	↓	Setze die Werte für $a$ , $b$ und $c$ ein.
	$=$	$\frac{- 16 m^{2} \pm \sqrt{(- 16 m^{2})^{2} - 4 \cdot (1 + m^{2}) \cdot 16 \cdot (4 m^{2} - 1)}}{2 \cdot (1 + m^{2})}$
	$=$	$\frac{- 16 m^{2} \pm \sqrt{256 m^{4} - 64 \cdot (1 + m^{2}) \cdot (4 m^{2} - 1)}}{2 \cdot (1 + m^{2})}$

Für die Tangente muss gelten, dass sie nur einen Berührpunkt mit dem Kreis haben darf. Daher darf es nur eine Lösung der Mitternachtsformel geben.

Um nur eine Lösung für die Gleichung

x_{1,2} = \frac{- 16 m^{2} \pm \sqrt{256 m^{4} - 64 \cdot (1 + m^{2}) \cdot (4 m^{2} - 1)}}{2 \cdot (1 + m^{2})}

zu erhalten, muss die Diskriminante $D = 256 m^{4} - 64 \cdot (1 + m^{2}) \cdot (4 m^{2} - 1)$ gleich $0$ sein.

$256 m^{4} - 64 \cdot (1 + m^{2}) \cdot (4 m^{2} - 1)$	$=$	$0$
	↓	Löse die Klammern auf.
$256 m^{4} - 64 \cdot (4 m^{2} - 1 + 4 m^{4} - m^{2})$	$=$	$0$
	↓	Fasse zusammen.
$256 m^{4} - 64 \cdot (4 m^{4} + 3 m^{2} - 1)$	$=$	$0$
	↓	Löse die Klammer auf.
$256 m^{4} - 256 m^{4} + 192 m^{2} - 64$	$=$	$0$	$+ 64$
	↓	Vereinfache.
$192 m^{2}$	$=$	$64$	$: 192$
	↓	Löse nach $m^{2}$ auf.
$m^{2}$	$=$	$\frac{64}{192}$
	↓	Kürze.
	$=$	$\frac{1}{3}$

Die Gleichung $m^{2} = \frac{1}{3}$ hat zwei Lösungen $m_{1} = \sqrt{\frac{1}{3}}$ und $m_{2} = - \sqrt{\frac{1}{3}} .$

Es gibt also zwei Geraden, die vom Punkt $P$ aus Tangenten an den Kreis sind:

$g_{1} : y = \sqrt{\frac{1}{3}} \cdot x + 8 \cdot \sqrt{\frac{1}{3}} \approx 0,58 x + 4,62$

$g_{2} : y = - \sqrt{\frac{1}{3}} \cdot x - 8 \cdot \sqrt{\frac{1}{3}} \approx - 0,58 x - 4,62$

Berührpunkt

Wenn $D = 0$ ist, dann gilt:

$x_{1,2} = \frac{- 16 m^{2} \pm \sqrt{0}}{2 \cdot (1 + m^{2})}$

Setze $m^{2} = \frac{1}{3}$ ein:

$x_{1,2}$	$=$	$\frac{- 16 \cdot \frac{1}{3}}{2 \cdot (1 + \frac{1}{3})}$
	↓	Fasse zusammen.
	$=$	$\frac{- \frac{16}{3}}{\frac{8}{3}}$
	$=$	$- 2$

Die $y$ -Werte der beiden Berührpunkte erhältst du, wenn $x = - 2$ in die Tangentengleichungen eingesetzt wird.

$y_{1} = \sqrt{\frac{1}{3}} \cdot (- 2) + 8 \cdot \sqrt{\frac{1}{3}} = 6 \cdot \sqrt{\frac{1}{3}} \approx 3,46$

$y_{2} = - \sqrt{\frac{1}{3}} \cdot (- 2) - 8 \cdot \sqrt{\frac{1}{3}} = - 6 \cdot \sqrt{\frac{1}{3}} \approx - 3,46$

Die beiden Berührpunkte haben die Koordinaten $B_{1} (- 2 | 3,46)$ und $B_{2} (- 2 | - 3,46)$ .

Graphische Darstellung

Die Abbildung ist in der Aufgabenstellung nicht verlangt worden.

Sie dient nur der Veranschaulichung.

Welche Punkte sind Berührpunkte (ein Schnittpunkt mit einer gemeinsamen Tangente und die beiden Graphen kreuzen sich nicht im Schnittpunkt)?
- B, D, F, G
- A, D, F, G
- B, C, D, E
- B, C, D, G
Punkt $A$ : Fall 1 transversales Schneiden
Punkt $B$ : Fall 3 Berührpunkt
Punkt $C$ : Fall 3 Berührpunkt
Punkt $D$ : Fall 3 Berührpunkt
Punkt $E$ : Fall 2 berührendes Schneiden
Punkt $F$ : Fall 1 transversales Schneiden
Punkt $G$ : Fall 3 Berührpunkt
Richtige Lösung: Berührpunkte sind die Punkte $B, C, D, G$ .

Gegeben ist ein Quader mit den Seiten $a = 8 cm$ , $b = 6 cm$ und $c = 4 cm$ .

Aus einer Quaderecke wird eine Pyramide herausgeschnitten. Die Schnitte verlaufen längs der Diagonalen der Seitenflächen.

a) Berechne jeweils die Flächeninhalte der vier Dreiecke $A_{1}$ , $A_{2}$ , $A_{3}$ und $A_{4}$ .

Hinweis: Verwende die Bezeichnungen von Bild 1 und Bild 3 und verwende für die Berechnung des Flächeninhalts von $A_{4}$ den Kosinussatz.

b) Weise nach, dass ${A_{1}}^{2} + {A_{2}}^{2} + {A_{3}}^{2} = {A_{4}}^{2}$ gilt.

Gegeben ist eine Ebenenschar $E_{a} : x_{1} + a \cdot x_{2} - x_{3} + 3 \cdot a = 0$ mit $a \in ℝ$ .

a) Die beiden Ebenen $E_{a_{1}}$ und $E_{a_{2}}$ sollen senkrecht aufeinander stehen.

Welche Beziehung besteht zwischen $a_{1}$ und $a_{2}$ ?

b) Zu welcher Ebene aus der oben angegebenen Schar gibt es keine dazu senkrechte Ebene aus dieser Schar?

c) Es ist $a \in ℝ^{+}$ . Berechne den Abstand $d (O, E_{a})$ des Koordinatenursprungs von der Scharebene $E_{a}$ und gib gegebenenfalls den Grenzwert $\lim_{a \to \infty} d (O, E_{a})$ an.

Lösung zu a)

Die beiden Ebenen haben folgende Gleichungen:

$E_{a_{1}} : x_{1} + a_{1} \cdot x_{2} - x_{3} + 3 \cdot a_{1} = 0$

$E_{a_{2}} : x_{1} + a_{2} \cdot x_{2} - x_{3} + 3 \cdot a_{2} = 0$

Lies die beiden Normalenvektoren ab:

${\vec{n}}_{a_{1}} = (\begin{array}{c} 1 \\ a_{1} \\ - 1 \end{array})$ und ${\vec{n}}_{a_{2}} = (\begin{array}{c} 1 \\ a_{2} \\ - 1 \end{array})$

Die beiden Ebenen $E_{a_{1}}$ und $E_{a_{2}}$ sollen senkrecht aufeinander stehen, dann muss das Skalarprodukt der beiden Normalenvektoren gleich null sein.

${\vec{n}}_{a_{1}} \circ {\vec{n}}_{a_{2}} = 0 \Rightarrow (\begin{array}{c} 1 \\ a_{1} \\ - 1 \end{array}) \circ (\begin{array}{c} 1 \\ a_{2} \\ - 1 \end{array}) = 0$

$(\begin{array}{c} 1 \\ a_{1} \\ - 1 \end{array}) \circ (\begin{array}{c} 1 \\ a_{2} \\ - 1 \end{array})$	$=$	$0$
	↓	Berechne das Skalarprodukt.
$1 \cdot 1 + a_{1} \cdot a_{2} + (- 1) \cdot (- 1)$	$=$	$0$
	↓	Fasse zusammen.
$2 + a_{1} \cdot a_{2}$	$=$	$0$	$- 2$
	↓	Löse nach $a_{1} \cdot a_{2}$ auf.
$a_{1} \cdot a_{2}$	$=$	$- 2$

Du hast die Gleichung $a_{1} \cdot a_{2} = - 2$ erhalten bzw. aufgelöst nach $a_{1}$ folgt:

a_{1} = - \frac{2}{a_{2}}

Wenn dieser Zusammenhang zwischen den beiden Scharparametern besteht, dann stehen die Scharebenen senkrecht aufeinander.

Lösung zu b)

Wenn $a_{2} = 0$ ist, dann müsste $a_{1} = - \frac{2}{0}$ sein. Das ist aber nicht möglich, da nicht durch $0$ geteilt werden darf.

Zu der Scharebene $E_{0} : x_{1} - x_{3} = 0$ mit $a_{2} = 0$ gibt es keine dazu senkrechte Ebene.

Lösung zu c)

Erstelle die Hessesche Normalenform der Ebene:

Wegen $a \in ℝ^{+}$ muss $E_{a} : x_{1} + a \cdot x_{2} - x_{3} + 3 \cdot a = 0$ mit $(- 1)$ multipliziert werden:

$x_{1} + a \cdot x_{2} - x_{3} + 3 \cdot a$	$=$	$0$	$\cdot (- 1)$
$- x_{1} - a \cdot x_{2} + x_{3} - 3 \cdot a$	$=$	$0$

Erstelle nun die Gleichung der Hesseschen Normalenform:

$E_{H N F} : \frac{- x_{1} - a \cdot x_{2} + x_{3} - 3 \cdot a}{\| \vec{n} \|}$	$=$	$0$
	↓	Setze den Normalenvektor ein.
$\frac{- x_{1} - a \cdot x_{2} + x_{3} - 3 \cdot a}{\sqrt{(- 1)^{2} + (- a)^{2} + 1^{2}}}$	$=$	$0$
	↓	Fasse zusammen.
$\frac{- x_{1} - a \cdot x_{2} + x_{3} - 3 \cdot a}{\sqrt{2 + a^{2}}}$	$=$	$0$

Für die Berechnung des Abstandes $d$ der Ebene vom Koordinatenursprung setze in $E_{H N F}$ die Koordinaten des Ursprungs $O (0 | 0 | 0)$ ein:

$d (O, E)$	$=$	$\| \frac{- 0 - a \cdot 0 + 0 - 3 \cdot a}{\sqrt{2 + a^{2}}} \|$
	↓	Fasse zusammen.
	$=$	$\| \frac{- 3 \cdot a}{\sqrt{2 + a^{2}}} \|$

Es ist $d (O, E) = | \frac{- 3 \cdot a}{\sqrt{2 + a^{2}}} | .$ Wegen $a \in ℝ^{+}$ erhältst du für den Betrag:

d (O, E) = \frac{3 \cdot a}{\sqrt{2 + a^{2}}}

Die Scharebene $E_{a}$ hat vom Koordinatenursprung den Abstand $d = \frac{3 \cdot a}{\sqrt{2 + a^{2}}}$ .

Berechnung des Grenzwertes von d(O,E)

\lim_{a \to \infty} d (O, E_{a})

=

\lim_{a \to \infty} \frac{3 \cdot a}{\sqrt{2 + a^{2}}}

	$\lim_{a \to \infty} \frac{3 \cdot a}{\sqrt{2 + a^{2}}}$
	↓ Klammere in Nenner $a^{2}$ aus.
$=$	$\lim_{a \to \infty} \frac{3 \cdot a}{\sqrt{a^{2} (\frac{2}{a^{2}} + 1)}}$
	↓ Schreibe den Nenner als Produkt von zwei Wurzeln.
$=$	$\lim_{a \to \infty} \frac{3 \cdot a}{\sqrt{a^{2}} \cdot \sqrt{\frac{2}{a^{2}} + 1}}$
	↓ Berechne $\sqrt{a^{2}}$ . Wegen $a \in ℝ^{+}$ ist $\sqrt{a^{2}} = a$ .
$=$	$\lim_{a \to \infty} \frac{3 \cdot a}{a \cdot \sqrt{\frac{2}{a^{2}} + 1}}$
	↓ Kürze mit $a$ .
$=$	$\lim_{a \to \infty} \frac{3}{\sqrt{\frac{2}{a^{2}} + 1}}$

Berechne den Grenzwert:

$\lim_{a \to \infty} \frac{3}{\sqrt{\underset{\to 0}{\underset{⏟}{\frac{2}{a^{2}}}} + 1}} = \frac{3}{\sqrt{1}} = 3$

Der Grenzwert $\lim_{a \to \infty} d (O, E_{a}) = 3$ .

Beziehungen zwischen den Winkelfunktionen
$\begin{array}{l} \tan \\ \cot \end{array}$
gegeben
gegeben
gegeben
$\cot φ$
$\frac{1}{\pm \sqrt{1 + \cot^{2} φ}}$
$\frac{\cot φ}{\sqrt{1 + \cot^{2} φ}}$
$\frac{1}{\cot φ}$
$? ? \cot φ =$
$\frac{\pm \sqrt{1 - \sin^{2} φ}}{\sin φ}$
$\frac{\cos φ}{\pm \sqrt{1 - \cos^{2} φ}}$
$\frac{1}{\tan φ}$
$\cot φ$
Beziehungen zwischen Sinus, Kosinus, Tangens und Kotangens
$\tan α \cdot \cot α = 1$
$\tan α = \frac{\sin α}{\cos α} = \frac{1}{\cot α}$
$\cot α = \frac{\cos α}{\sin α} = \frac{1}{\tan α}$
$1 + \tan^{2} α = \frac{1}{\cot^{2} α}$
$1 + \cot^{2} α = \frac{1}{\sin^{2} α}$
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
Du kannst dann die vorhandene Zeichnung weiterer benutzen.
(Alternativ kannst du auch das Koordinatensystem (mit der Geraden) in dein Heft übertragen.)
Alternativ kannst du auch die Abbildung in dein Heft übertragen.

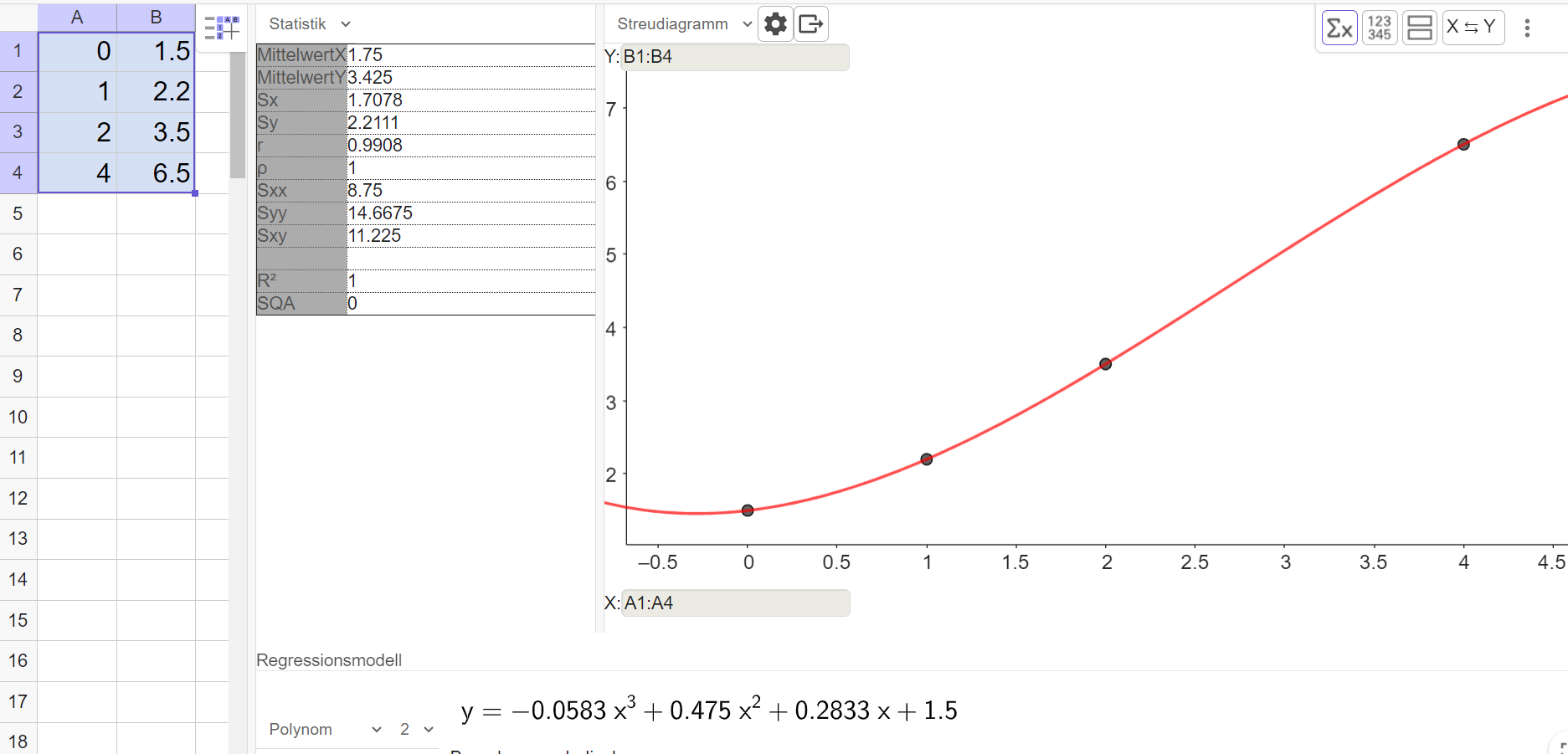
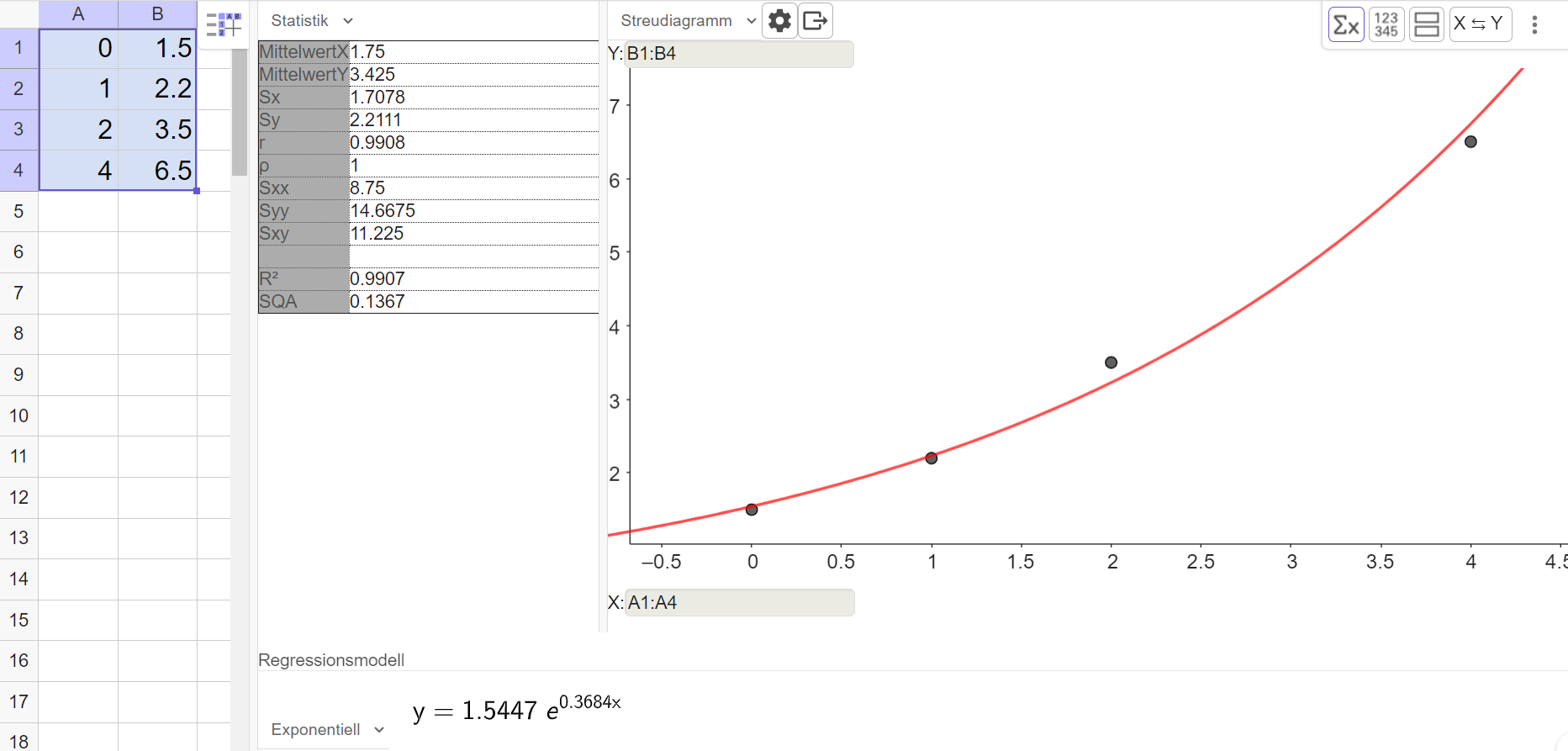
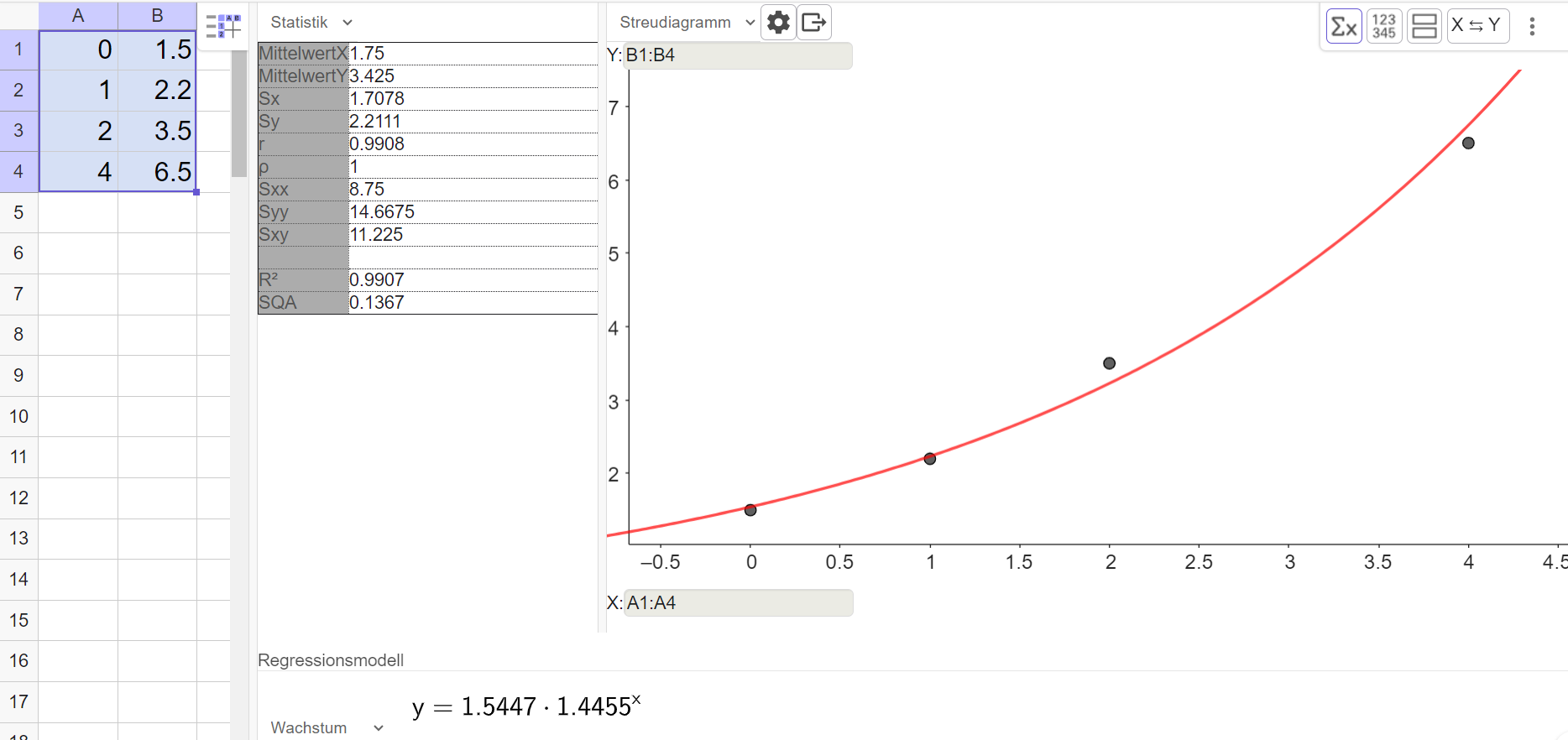
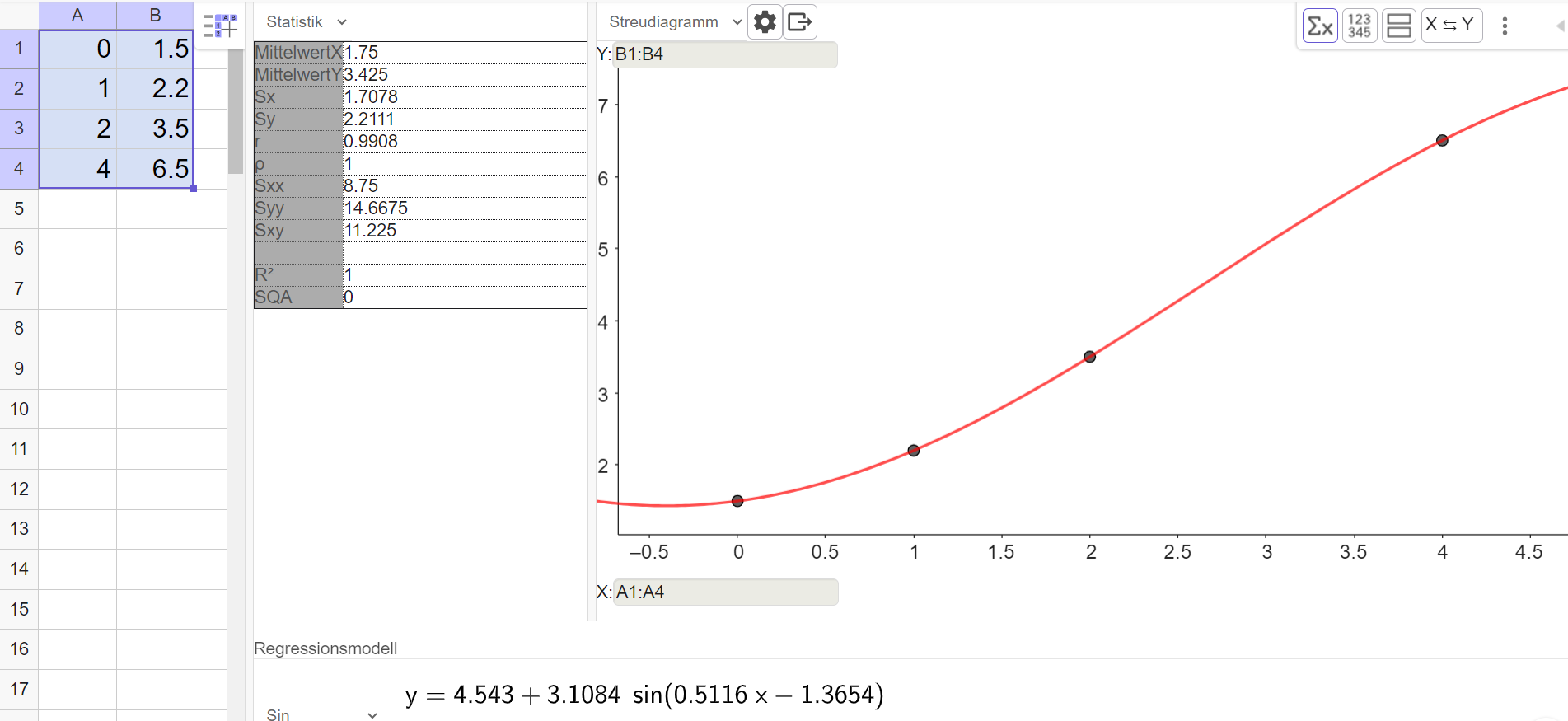
11
Entscheide anhand des Graphens, ob der gegebene Graph der Funktion
achsensymmetrisch zur y-Achse oder
punktsymmetrisch zum Koordinatenursprung $O (0 | 0)$
ist.
punktsymmetrisch zu $O (0 | 0)$
achsensymmetrisch zur y-Achse

Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie
Der Graph ist achsensymmetrisch zur y-Achse.
Zusätzliche Erläuterung:
In der Abbildung ist die Symmetrieachse eingezeichnet.
Der Graph auf der linken Seite der y-Achse ist ein Spiegelbild der rechten Seite.
Die Symmetrieachse ist die $y$ -Achse.
Also ist die Funktion achsensymmetrisch zur $y$ -Achse.

punktsymmetrisch zu $O (0 | 0)$
achsensymmetrisch zur y-Achse

Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie
Der Graph ist punktsymmetrisch zu $O (0 | 0)$ .
Zusätzliche Erläuterung:
1. Möglichkeit für den Nachweis der Punktsymmetrie zu $O (0 | 0)$
Bei Punktsymmetrie zum Ursprung wird der Punkt $A$ auf den Punkt $A^{'}$ abgebildet. Ebenso wird der Punkt $B$ auf $B^{'}$ abgebildet. Das gilt für alle Punkte des Graphen.
Also ist der Graph punktsymmetrisch zu $O (0 | 0)$ .
2. Möglichkeit für den Nachweis der Punktsymmetrie zu $O (0 | 0)$
Dreht man den Graphen um $180^{\circ}$ um
um den Koordinatenursprung $O (0 | 0)$ , dann wird der Graph auf sich selbst abgebildet.
$\Rightarrow$ Der Graph ist punktsymmetrisch zum Ursprung.

punktsymmetrisch zu $O (0 | 0)$
achsensymmetrisch zur y-Achse

Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie
Der Graph ist achsensymmetrisch zur y-Achse.
Zusätzliche Erläuterung:
In der Abbildung ist die Symmetrieachse eingezeichnet.
Der Graph auf der linken Seite der y-Achse ist ein Spiegelbild der rechten Seite.
Die Symmetrieachse ist die $y$ -Achse.
Also ist die Funktion achsensymmetrisch zur $y$ -Achse.

punktsymmetrisch zu $O (0 | 0)$
achsensymmetrisch zur y-Achse

Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie
Der Graph ist punktsymmetrisch zu $O (0 | 0)$ .
Zusätzliche Erläuterung:
1. Möglichkeit für den Nachweis der Punktsymmetrie zu $O (0 | 0)$
Bei Punktsymmetrie zum Ursprung wird der Punkt $A$ auf den Punkt $A^{'}$ abgebildet. Ebenso wird der Punkt $B$ auf $B^{'}$ abgebildet. Das gilt für alle Punkte des Graphen.
Also ist der Graph punktsymmetrisch zu $O (0 | 0)$ .
2. Möglichkeit für den Nachweis der Punktsymmetrie zu $O (0 | 0)$
Dreht man den Graphen um $180^{\circ}$ um
um den Koordinatenursprung $O (0 | 0)$ , dann wird der Graph auf sich selbst abgebildet.
$\Rightarrow$ Der Graph ist punktsymmetrisch zum Ursprung.

punktsymmetrisch zu $O (0 | 0)$
achsensymmetrisch zur y-Achse

Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie
Der Graph ist achsensymmetrisch zur y-Achse.
Zusätzliche Erläuterung:
In der Abbildung ist die Symmetrieachse eingezeichnet.
Der Graph auf der linken Seite der y-Achse ist ein Spiegelbild der rechten Seite.
Die Symmetrieachse ist die $y$ -Achse.
Also ist die Funktion achsensymmetrisch zur $y$ -Achse.

punktsymmetrisch zu $O (0 | 0)$
achsensymmetrisch zur y-Achse

Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie
Der Graph ist punktsymmetrisch zu $O (0 | 0)$ .
Zusätzliche Erläuterung:
1. Möglichkeit für den Nachweis der Punktsymmetrie zu $O (0 | 0)$
Bei Punktsymmetrie zum Ursprung wird der Punkt $A$ auf den Punkt $A^{'}$ abgebildet. Ebenso wird der Punkt $B$ auf $B^{'}$ abgebildet. Das gilt für alle Punkte des Graphen.
Also ist der Graph punktsymmetrisch zu $O (0 | 0)$ .
2. Möglichkeit für den Nachweis der Punktsymmetrie zu $O (0 | 0)$
Dreht man den Graphen um $180^{\circ}$
um den Koordinaten-ursprung $O (0 | 0)$ , dann wird der Graph auf sich selbst abgebildet.
$\Rightarrow$ Der Graph ist punktsymmetrisch zum Ursprung.
12
Entscheide graphisch, welche der jeweils angegebenen Aussagen auf den Graphen zutrifft.
Der Graph ist achsensymmetrisch zur y-Achse.
Der Graph hat keine Symmetrie.
Der Graph ist punktsymmetrisch zu $O (0 | 0)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie
Der Graph ist punktsymmetrisch zu $O (0 | 0)$ .
Zusätzliche Erläuterung:
1. Möglichkeit für den Nachweis der Punktsymmetrie zu $O (0 | 0)$
Bei Punktsymmetrie zum Ursprung wird der Punkt $A$ auf den Punkt $A^{'}$ abgebildet. Ebenso wird der Punkt $B$ auf $B^{'}$ abgebildet. Das gilt für alle Punkte des Graphen.
Also ist der Graph punktsymmetrisch zu $O (0 | 0)$ .
2. Möglichkeit für den Nachweis der Punktsymmetrie zu $O (0 | 0)$
Dreht man den Graphen um $180^{\circ}$ um den Koordinatenursprung $O (0 | 0)$ , dann wird der Graph auf sich selbst abgebildet.
$\Rightarrow$ Der Graph ist punktsymmetrisch zum Ursprung.

Der Graph ist punktsymmetrisch zum Punkt $P (- 3 | 4)$ .
Der Graph ist achsensymmetrisch zur y-Achse.
Der Graph hat keine Symmetrie.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie
Der Graph ist punktsymmetrisch zum Punkt $P (- 3 | 4)$ .
Zusätzliche Erläuterung:
1. Möglichkeit für den Nachweis der Punktsymmetrie zu $P (- 3 | 4)$
Bei Punktsymmetrie zum Punkt $P (- 3 | 4)$ wird der Punkt $A$ auf den Punkt $A^{'}$ abgebildet. Ebenso wird der Punkt $B$ auf $B^{'}$ abgebildet. Das gilt für alle Punkte des Graphen.
Also ist der Graph punktsymmetrisch zum Punkt $P (- 3 | 4)$ .
2. Möglichkeit für den Nachweis der Punktsymmetrie zu $P (- 3 | 4)$
Dreht man den Graphen um $180^{\circ}$ um den Punkt $P (- 3 | 4)$ , dann wird der Graph auf sich selbst abgebildet.
$\Rightarrow$ Der Graph ist punktsymmetrisch zum Punkt $P (- 3 | 4)$ .

Der Graph ist achsensymmetrisch zur Geraden $x = 4$ .
Der Graph ist punktsymmetrisch zu $O (0 | 0)$ .
Der Graph hat keine Symmetrie.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie
Der Graph ist achsensymmetrisch zur Geraden $x = 4$ .
Zusätzliche Erläuterung:
In der Abbildung ist die Symmetrieachse $x = 4$ eingezeichnet.
Der Graph auf der linken Seite der Symmetrieachse ist ein Spiegelbild der rechten Seite.
Also ist die Funktion achsensymmetrisch zur Geraden $x = 4$ .

Der Graph hat keine Symmetrie.
Der Graph ist achsensymmetrisch zur y-Achse
Der Graph ist punktsymmetrisch zu $O (0 | 0)$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie
Der Graph ist nicht symmetrisch.
Zusätzliche Erläuterung:
Es gibt keine Symmetrieachse und es gibt keinen Punkt zu dem der Graph der Funktion achsensymmetrisch bzw. punktsymmetrisch ist.
$\Rightarrow$ Es liegt keine Symmetrie vor.

Der Graph hat keine Symmetrie.
Der Graph ist punktsymmetrisch zu $O (0 | 0)$ .
Der Graph ist achsensymmetrisch zur y-Achse.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie
Der Graph ist achsensymmetrisch zur y-Achse.
Zusätzliche Erläuterung:
In der Abbildung ist die Symmetrieachse eingezeichnet.
Der Graph auf der linken Seite der y-Achse ist ein Spiegelbild der rechten Seite.
Die Symmetrieachse ist die $y$ -Achse.
Also ist die Funktion achsensymmetrisch zur $y$ -Achse.

	$\tan α \cdot \cot α = 1$	$\tan α = \frac{\sin α}{\cos α} = \frac{1}{\cot α}$
$\cot α = \frac{\cos α}{\sin α} = \frac{1}{\tan α}$	$1 + \tan^{2} α = \frac{1}{\cot^{2} α}$	$1 + \cot^{2} α = \frac{1}{\sin^{2} α}$

Kowalskys zweite Testaufgabe

Test

Lineare Funktion
Eine Funktion $f$ mit $y = f (x) = m x + b$ heißt lineare Funktion. Der Graph einer linearen Funktion ist eine Gerade.
Die Zahl $m$ gibt die Steigung der Geraden an.
$m > 0$ : Gerade ist streng monoton steigend.
$m < 0$ : Gerade ist streng monoton fallend.
$m = \frac{Δ y}{Δ x} = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} = \tan φ$
Die Zahl $b$ ist der y-Achsenabschnitt.
Die y-Achse wird bei $b$ geschnitten: $x = 0 \Rightarrow S_{y} (0 | b)$
Nullstelle: $y = 0 \Rightarrow N (- \frac{n}{m} | 0)$
Zweipunkteform der Geradengleichung
Gegeben sind die Punkte $P_{1} (x_{1} | y_{1}), P_{2} (x_{2} | y_{2})$ :
$y = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \cdot (x - x_{1}) + y_{1}$

Gilt für die Steigungen $m_{g}$ und $m_{h}$ von zwei Geraden $g$ und $h$ , dass $m_{g} \cdot m_{h} = - 1$ ist, dann stehen die Geraden senkrecht aufeinander.
Quadratische Funktion
Normalform
Eine Funktion $f$ mit $y = f (x) = x^{2} + p x + q$ und $(p, q \in ℝ)$ heißt quadratische Funktion.
Definitionsmenge: $x \in ℝ$
Wertemenge: $y \in ℝ; y \geq q - {(\frac{p}{2})}^{2}$
Der Graph einer quadratischen Funktion ist eine Parabel mit dem Scheitelpunkt
$S (- \frac{p}{2} | q - {(\frac{p}{2})}^{2})$ .
Nullstellen: $x_{1,2} = - \frac{p}{2} \pm \sqrt{{(\frac{p}{2})}^{2} - q}$
Schnittpunkt mit y-Achse: $S_{y} (0 | q)$
Allgemeine Form
$y = f (x) = a x^{2} + b x + c$
$(a, b, c \in ℝ (konst.); a \neq 0)$
Definitionsmenge: $x \in ℝ$
Wertemenge: $y \in ℝ; y \geq \frac{4 a c - b^{2}}{4 a} für a > 0; y < \frac{4 a c - b^{2}}{4 a} für a < 0$
Der Graph einer quadratischen Funktion ist eine Parabel mit dem Scheitelpunkt
$S (- \frac{b}{2 a} | c - \frac{b^{2}}{4 a})$ .
Nullstellen: $x_{1, 2} = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$
Schnittpunkt mit y-Achse: $S_{y} (0 | c)$
Scheitelpunktform
$y = f (x) = a (x - d)^{2} + e$
Definitionsmenge: $x \in ℝ$
Wertemenge: $y \in ℝ; y \geq e$
Nullstellen: $x_{1, 2} = d \pm \sqrt{- e}$
Schnittpunkt mit y-Achse: $S_{y} (0 | d^{2} + e)$
Scheitelpunkt: $S (d | e)$
..
$\begin{array}{l} 227,50 : 7 = 32,5 \\ - 21 \\ 17 \\ - 14 \\ 35 \\ - 35 \\ 0 \end{array}$

Die Koordinatenform der Geradengleichung lautet:

$a x + b y = c$

Wenn $2$ Punkte $P_{1} (x_{1} | y_{1})$ und $P_{2} (x_{2} | y_{2})$ auf der Geraden gegeben sind, kann man die Parameter der Koordinatenform wie folgt berechnen:

$\begin{array}{l} a = y_{1} - y_{2} \\ b = x_{2} - x_{1} \\ c = x_{2} y_{1} - x_{1} y_{2} \end{array}$

Wie kommt man auf diese Berechnung der drei Parameter $a, b$ und $c$ ?

Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unsererDatenschutzerklärung.

14
Prozentrechnung im Sandkasten
Im Sandkasten sind 20% der Fläche mit Spielzeug bedeckt. Wenn der Sandkasten insgesamt eine Fläche von $100 m^{2}$ hat, wie groß ist die Fläche, die mit Spielzeug bedeckt ist?
$5 m^{2}$
$10 m^{2}$
$20 m^{2}$
$40 m^{2}$

Zuerst den Prozentsatz in eine Dezimalzahl umwandeln, indem man durch 100 teilt: $20 % = \frac{20}{100} = 0,20$ .
Dann die Gesamtfläche des Sandkastens mit der Dezimalzahl multiplizieren, um die bedeckte Fläche zu berechnen: $100 m^{2} \times 0,20 = 20 m^{2}$ .
Denke daran, den Prozentsatz zuerst in eine Dezimalzahl umzuwandeln und dann mit der Gesamtfläche zu multiplizieren.
15
Anwendung des Strahlensatzes
Ein Baum wirft einen 4,5 m langen Schatten, während ein 1,2 m hoher Pfosten im selben Licht einen 1,6 m langen Schatten wirft. Wie hoch ist der Baum?
$3,375 m$
$2,7 m$
$5,4 m$
$6,75 m$

Schreibe die Verhältnisgleichung auf, die sich aus dem Strahlensatz ergibt: $\frac{Höhe des Baumes}{Schattenlänge des Baumes} = \frac{Höhe des Pfostens}{Schattenlänge des Pfostens}$ .
Setze die bekannten Werte in die Gleichung ein: $\frac{Höhe des Baumes}{4,5 m} = \frac{1,2 m}{1,6 m}$ .
Löse die Gleichung nach der Höhe des Baumes auf: $Höhe des Baumes = \frac{1,2 m \cdot 4,5 m}{1,6 m}$ .
Führe die Multiplikation und Division aus: $Höhe des Baumes = \frac{5,4}{1,6}$ .
Berechne das Ergebnis: $Höhe des Baumes = 3,375 m$ .
Überprüfe die Verhältnisse und stelle sicher, dass du die Werte korrekt in die Verhältnisgleichung einsetzt. Achte auf die Einheiten und führe die Berechnungen sorgfältig durch.
16
Single-Choice-Aufgabe zur Kurvendiskussion des Medikamentenabbaus
Betrachten Sie die Funktion $f (t) = e^{- 0.5 t}$ , die den Medikamentenabbau im Körper über die Zeit $t$ beschreibt. Wie groß ist die momentane Änderungsrate des Medikamentenabbaus zum Zeitpunkt $t = 2$ ?
$- 0.5 e^{- 0.5 i m e s 2}$
$- e^{- 0.5 i m e s 2}$
$e^{- 0.5 i m e s 2}$
$- 0.25 e^{- 0.5 i m e s 2}$

Um die momentane Änderungsrate zu bestimmen, muss die erste Ableitung der Funktion $f (t)$ berechnet werden.
Die erste Ableitung einer Exponentialfunktion $f (t) = e^{k t}$ , wobei $k$ eine Konstante ist, ist $f^{'} (t) = k i m e s e^{k t}$ .
Wenden Sie die Regel zur Ableitung der Exponentialfunktion auf $f (t) = e^{- 0.5 t}$ an, um die Ableitung zu erhalten: $f^{'} (t) = - 0.5 i m e s e^{- 0.5 t}$ .
Setzen Sie $t = 2$ in die Ableitung $f^{'} (t)$ ein, um die momentane Änderungsrate zu diesem Zeitpunkt zu finden: $f^{'} (2) = - 0.5 i m e s e^{- 0.5 i m e s 2}$ .
Überprüfen Sie Ihre Berechnungen sorgfältig und stellen Sie sicher, dass Sie die richtige Regel für die Ableitung der Exponentialfunktion verwenden.
17
Kurvendiskussion einer Exponentialfunktion
Bestimme die Nullstelle der Funktion $f (x) = e^{x} - 3$ .
$x = 3$
$x = e^{3}$
$x = 0$
$x = \ln (3)$

Setze die Funktion gleich Null: $e^{x} - 3 = 0$ .
Addiere 3 auf beiden Seiten der Gleichung: $e^{x} = 3$ .
Wende den natürlichen Logarithmus auf beiden Seiten an: $x = \ln (3)$ .
Vergiss nicht, den natürlichen Logarithmus zu verwenden, um die e-Funktion zu invertieren.

Ermittle das lokale Extremum der Funktion $f (x) = - 2 e^{- 0.5 x}$ .
$x = 0$
$x = - 2$
$x = - 0.5$
$x = 1$

Bilde die erste Ableitung der Funktion: $f^{'} (x) = 2 \cdot 0.5 \cdot e^{- 0.5 x}$ .
Setze die erste Ableitung gleich Null: $2 \cdot 0.5 \cdot e^{- 0.5 x} = 0$ .
Da $e^{- 0.5 x}$ niemals Null wird, ist das Extremum bei $x = 0$ .
Denke daran, dass die e-Funktion niemals den Wert Null annimmt.

Finde den Wendepunkt der Funktion $f (x) = e^{2 x} - x$ .
$x = 0$
$x = \frac{1}{2}$
$x = \frac{1}{4}$
$x = 1$

Bilde die erste Ableitung: $f^{'} (x) = 2 e^{2 x} - 1$ .
Bilde die zweite Ableitung: $f^{''} (x) = 4 e^{2 x}$ .
Setze die zweite Ableitung gleich Null: $4 e^{2 x} = 0$ , was keine Lösung hat.
Da die zweite Ableitung immer positiv ist, gibt es keinen Wendepunkt.
Erinnere dich, dass ein Wendepunkt dort ist, wo die zweite Ableitung ihr Vorzeichen wechselt.

Bestimme das asymptotische Verhalten der Funktion $f (x) = \frac{e^{x}}{x^{2} + 1}$ für $x \to \infty$ .
$f (x) \to \infty$
$f (x) \to e$
$f (x) \to 0$
$f (x) \to 1$

Betrachte den Nenner $x^{2} + 1$ , der schneller wächst als der Zähler $e^{x}$ , wenn $x \to \infty$ .
Daher nähert sich der Quotient Null, wenn $x$ gegen Unendlich geht.
Vergleiche die Wachstumsgeschwindigkeiten von Zähler und Nenner für $x \to \infty$.

Wie verhält sich der Graph der Funktion $f (x) = - 3 e^{x}$ im Unendlichen?
Er nähert sich der x-Achse von oben.
Er nähert sich der x-Achse von unten.
Er strebt gegen Unendlich.
Er bleibt konstant.

Da der Koeffizient vor $e^{x}$ negativ ist, wird der Graph im Unendlichen immer weiter fallen.
Somit nähert sich der Graph der x-Achse von unten an.
Beachte das Vorzeichen vor der e-Funktion, um das Verhalten im Unendlichen zu bestimmen.
18
Kurvendiskussion einer e-Funktion
Welche Art von Extrempunkt hat die Funktion $f (x) = e^{2 x} - 3 e^{x}$ bei $x = \ln (\frac{3}{2})$ ?
$Minimum$
$Maximum$
$Sattelpunkt$
$Kein Extrempunkt$

Betrachte die Funktion $f (x) = e^{2 x} - 3 e^{x}$ .
Bestimme die erste Ableitung $f^{'} (x) = 2 e^{2 x} - 3 e^{x}$ .
Bestimme die zweite Ableitung $f^{''} (x) = 4 e^{2 x} - 3 e^{x}$ .
Setze die erste Ableitung gleich Null, um die Extremstellen zu finden: $2 e^{2 x} - 3 e^{x} = 0$ .
Faktorisiere die Gleichung, indem du $e^{x}$ ausklammerst: $e^{x} (2 e^{x} - 3) = 0$ .
Löse die Gleichung $e^{x} = 0$ und $2 e^{x} - 3 = 0$ .
Die Gleichung $e^{x} = 0$ hat keine Lösung, da die e-Funktion niemals Null wird.
Löse die Gleichung $2 e^{x} - 3 = 0$ nach $x$ auf: $e^{x} = \frac{3}{2}$ , dann $x = \ln (\frac{3}{2})$ .
Setze $x = \ln (\frac{3}{2})$ in die zweite Ableitung ein, um das Krümmungsverhalten zu prüfen.
Bestimme die y-Koordinate des Extrempunkts, indem du $x = \ln (\frac{3}{2})$ in die Ausgangsfunktion einsetzt.
Beachte die Eigenschaften der e-Funktion und löse Schritt für Schritt. Überprüfe jede Ableitung und Gleichung sorgfältig.
19
NRW 2024
Aufgabe 1
Ein Fan des VfL Bochum möchte mit einem mathematischen Modell den Besucheransturm beim nächsten Heimspiel beschreiben. Der Ansturm der Besucher wird (in Tausend Zuschauern pro Stunde) näherungsweise beschrieben durch die Funktion $f$ mit $f (x) = 120 x \cdot e^{- 2 x}$ . Dabei stellt $x = 0$ den Zeitpunkt der Öffnung des Stadions um 14.00 Uhr dar. Das Spiel wird anderthalb Stunden später angepfiffen, also bei $x = 1,5$ .
Geben Sie an, wie groß der Besucheransturm um 14.15 Uhr und um 15.00 Uhr ist. Rechnen Sie das Ergebnis auch in Besucher pro Minute um.

Berechnen Sie, zu welchem Zeitpunkt der Besucheransturm am größten ist.
(zur Kontrolle: $f^{'} (x) = 120 \cdot (1 - 2 x) \cdot e^{- 2 x}$ )

Beschreiben Sie, mit welchen Transformationen der Graph der Ableitungsfunktion $f^{'}$ aus dem Graphen der Funktion $f$ entsteht.
20
NRW 2024
Aufgabe 2
Gegeben ist die ganzrationale Funktion $f$ mit $f (x) = x^{3} - 3 b x$ , $b > 0$ .
Zeigen Sie, dass der Graph der Funktion $f$ punktsymmetrisch ist.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie von Graphen
Zeige, dass der Graph der Funktion $f$ punktsymmetrisch ist
Möglichkeit 1
Der Funktionsterm enthält nur ungerade Exponenten. Der Graph der Funktion ist demnach punktsymmetrisch zum Koordinatenursprung.
Möglichkeit 2
Wenn $f (- x) = - f (x)$ ist, dann ist der Graph der Funktion punktsymmetrisch zum Koordinatenursprung:
$f (- x) = (- x)^{3} - 3 b (- x) = - x^{3} + 3 b x = - (x^{3} - 3 b x) = - f (x)$
Also gilt $f (- x) = - f (x)$ .

Durch den Tief- und den Hochpunkt des Graphen werden Geraden gezeichnet, die parallel zu den Achsen verlaufen; diese schließen dann mit den Achsen des Koordinatensystems eine rechteckige Fläche ein. Für welchen Parameterwert $b$ ergibt sich ein Quadrat?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadrat
Für welchen Parameterwert $b$ ergibt sich ein Quadrat?
Berechne die Koordinaten des Hoch- und Tiefpunktes.
$f^{'} (x) = 3 x^{2} - 3 b$
$f^{'} (x) = 0 \Rightarrow 0 = 3 x^{2} - 3 b \Rightarrow x = \pm \sqrt{b}$
$f (- \sqrt{b}) = - b \sqrt{b} - 3 b (- \sqrt{b}) = 2 b \sqrt{b}$
$f (\sqrt{b}) = b \sqrt{b} - 3 b (\sqrt{b}) = - 2 b \sqrt{b}$
Ein Quadrat liegt vor, wenn $Δ x = Δ y$
$Δ x = \sqrt{b} - (- \sqrt{b}) = 2 \sqrt{b}$
$Δ y = 2 b \sqrt{b} - (- 2 b \sqrt{b}) = 4 b \sqrt{b}$
$\Rightarrow 2 \sqrt{b} = 4 b \sqrt{b} \Rightarrow b = \frac{1}{2}$
Für $b = \frac{1}{2}$ ergibt sich ein Quadrat.
Die folgende Abbildung ist in der Aufgabenstellung nicht gefordert. Sie dient nur zur Veranschaulichung.
21
NRW 2024
Aufgabe 3
Die Funktion f ist gegeben durch $f (x) = x^{3}$ .
Zeigen Sie, dass die Tangente $t$ im Punkt $P (1 | 1)$ an den Graphen der Funktion $f$ durch die Gleichung $t (x) = 3 x - 2$ beschrieben werden kann.

Zeigen Sie, dass die Tangente $t$ und der Graph von $f$ auch den Punkt $P (- 2 | - 8)$ gemeinsam haben.

Fertigen Sie zu a), b) eine Skizze an.

Bestimmen Sie den Flächeninhalt des Dreiecks, das durch die y-Achse, die x-Achse und die Tangente eingeschlossen wird.

Bestimmen Sie den Flächeninhalt der Fläche, die von den Graphen von $f$ und $t$ eingeschlossen wird.
22
A 1.0 Die Funktion $f_{1}$ hat die Gleichung $y = \log_{3} (x - 1,5) + 0,5$ mit $𝔾 = ℝ \times ℝ$ .
A 1.1 Bestimmen Sie die nach y aufgelöste Gleichung der Umkehrfunktion zu $1$ .
A 1.2 Der Graph der Funktion $f_{1}$ wird durch Parallelverschiebung mit dem Vektor
$\vec{v} = (\binom{v_{x}}{0}) (v_{x} \in ℝ)$ auf den Graphen der Funktion $f_{2}$ abgebildet, wobei der Punkt $P (- 3 | 2,5)$ auf dem Graphen zu $f_{2}$ liegt.
23
Pflichtteil Teil A
Aufgabe 1
Gegeben ist die Funktion $f$ mit $f (x) = (\frac{1}{2} x^{2} - \frac{1}{2} x - \frac{7}{4}) \cdot e^{2 x + 1}, x \in ℝ$ .
Weise nach: $f^{'} (x) = (x^{2} - 4) \cdot e^{2 x + 1}$ . (2 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Benutze die Produktregel und beachte beim Ableiten der e-Funktion die Kettenregel:
$(u (x) \cdot v (x))^{'} = u^{'} (x) \cdot v (x) + u (x) \cdot v^{'} (x)$
Es ist $u (x) = \frac{1}{2} x^{2} - \frac{1}{2} x - \frac{7}{4}$ und $v (x) = e^{2 x + 1}$
Dann ist $u^{'} (x) = x - \frac{1}{2}$ und $v^{'} (x) = 2 \cdot e^{2 x + 1}$
Setze in die Formel für die Produktregel ein.
Dann folgt:
$f^{'} (x) = (x - \frac{1}{2}) \cdot e^{2 x + 1} + (\frac{1}{2} x^{2} - \frac{1}{2} x - \frac{7}{4}) \cdot 2 \cdot e^{2 x + 1}$
$f^{'} (x)$ $=$ $(x - \frac{1}{2}) \cdot e^{2 x + 1} + (\frac{1}{2} x^{2} - \frac{1}{2} x - \frac{7}{4}) \cdot 2 \cdot e^{2 x + 1}$
↓
Klammere $e^{2 x + 1}$ aus. Multipliziere die $2$ in die hintere Klammer.
$=$ $e^{2 x + 1} (x - \frac{1}{2} + x^{2} - x - \frac{7}{2})$
↓
Fasse zusammen.
$=$ $e^{2 x + 1} (x^{2} - 4)$
Damit ist gezeigt, dass gilt: $f^{'} (x) = (x^{2} - 4) \cdot e^{2 x + 1}$
Benutze die Produktregel und beachte beim Ableiten der e-Funktion die Kettenregel.

Untersuche die Funktion $f$ auf lokale Extremstellen. (3 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
Eine lokale Extremstelle $x_{E}$ einer differenzierbaren Funktion ist eine Nullstelle der Ableitung: $f^{'} (x_{E} ) = 0$ .
Es gilt: $f^{'} (x) = (x^{2} - 4) \cdot e^{2 x + 1}$
$f^{'} (x_{E} ) = 0 \Rightarrow 0 = (x^{2} - 4) \cdot e^{2 x + 1}$
Zur Lösung der Gleichung verwende den Satz vom Nullprodukt:
$e^{2 x + 1}$ ist für alle $x \neq 0$ .
Dann bleibt nur der andere Term, der null werden kann:
$x^{2} - 4 = 0$ $\Rightarrow$ $x_{E_{1}} = - 2$ und $x_{E_{2}} = 2$
Anstatt die zweite Ableitung zu berechnen, kann man auch mit dem Vorzeichenwechselkriterium die Art einer möglichen Extremstelle $x_{E} $ bestimmen, dabei berechnet man das Monotonieverhalten der Funktion.
Berechne die Ableitungen an den Stellen $x = - 3$ , $x = 0$ und $x = 3$ .
$f^{'} (- 3) = ((- 3)^{2} - 4) \cdot e^{2 \cdot (- 3) + 1} = 5 \cdot e^{- 5} > 0$
$f^{'} (0) = (0^{2} - 4) \cdot e^{2 \cdot 0 + 1} = - 4 \cdot e^{1} < 0$
$f^{'} (3) = (3^{2} - 4) \cdot e^{2 \cdot 3 + 1} = 5 \cdot e^{7} > 0$
An der Stelle $x_{E_{1}} = - 2$ gibt es demnach einen Vorzeichenwechsel von $+ \mapsto -$ .
Hier liegt ein lokales Maximum vor.
An der Stelle $x_{E_{2}} = 2$ gibt es demnach einen Vorzeichenwechsel von $- \mapsto +$ .
Hier liegt ein lokales Minimum vor.
Eine lokale Extremstelle $x_{E}$ einer differenzierbaren Funktion ist eine Nullstelle der ersten Ableitung. Berechne $f^{'} (x_{E} ) = 0$ .
Bestimme mit dem Vorzeichenwechselkriterium die Art einer möglichen Extremstelle $x_{E} $ .
24
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 1
Ein mit Wasser befülltes Glas wird aus einem Kühlschrank genommen. Die anschließende Entwicklung der Wassertemperatur infolge der höheren Raumtemperatur lässt sich mithilfe der in $ℝ$ definierten Funktion $f : t \mapsto 25 - 20 \cdot e^{- 0,014 \cdot t}$ modellhaft beschreiben. Dabei ist $t$ die Zeit in Minuten, die seit der Entnahme aus dem Kühlschrank vergangen ist, und $f (t)$ die Wassertemperatur in $^{\circ} C$ . Die Raumtemperatur beträgt konstant $25^{\circ} C$ .
(i) Geben Sie die Wassertemperatur zum Zeitpunkt der Entnahme aus dem Kühlschrank an. (1 P)
(ii) Bestimmen Sie den Zeitpunkt, zu dem die Wassertemperatur $12^{\circ} C$ beträgt. (2 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: y-Achsenabschnitt
(i) Für GTR und CAS.
Berechne $f (0)$ .
(ii) Für GTR und CAS.
Löse die Gleichung $f (t) = 12$ .

Berechnen Sie die Werte der folgenden Terme und interpretieren Sie diese im Sachzusammenhang:
(i) $f^{'} (30)$ (2 P)(ii) $\frac{f (30) - f (0)}{30 - 0}$ (3 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Die mittlere Änderungsrate – Einführung der Ableitung
(i) Für GTR.
Betrachte den Graphen von $f (x)$ . (Beim GTR $x$ statt $t$ .)
Gib für $x$ den Wert $30$ ein.
Angezeigt wird $\frac{d Y}{d X}$ , die erste Ableitung an der Stelle $x = 30$ , also $f^{'} (30)$ .
(i) Für CAS.
Berechne $f^{'} (30)$ .
(ii) Für GTR.
Für die mittlere Änderungsrate gilt allgemein: $\frac{f (t_{2}) - f (t_{1})}{t_{2} - t_{1}}$
Setze $t_{2} = 30$ und $t_{1} = 0$ ein und vereinfache.
(ii) Für CAS.
Berechne $\frac{f (30) - 5}{30}$ .

Zeigen Sie, dass in diesem Modell gilt:
Es gibt eine Konstante $c$ , sodass zu jedem Zeitpunkt die Differenz zwischen der Raumtemperatur und der Wassertemperatur das $c$ -fache der momentanen Änderungsrate der Wassertemperatur ist. (4 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichungen
Für GTR.
Berechne $f^{'} (t)$ .
Löse die Gleichung $25 - f (t) = c \cdot f^{'} (t)$ nach $t$ auf.
Für CAS.
Löse die Gleichung $25 - f (t) = c \cdot f^{'} (t)$ nach $t$ auf.

Die folgende Rechnung stellt die Lösung einer Aufgabe im vorliegenden Sachzusammenhang dar:
Aus $f (t) = \frac{f (0) + 25}{2}$ ergibt sich $t \approx 49,5$ .
Formulieren Sie eine passende Aufgabenstellung. (3 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Aufgaben zum arithmetischen Mittel
Formuliere eine passende Aufgabenstellung
Berechnet wird mit $f (t) = \frac{f (0) + 25}{2}$ ein Mittelwert.
Aufgabenstellung:
Berechne den Zeitpunkt, zu dem die Wassertemperatur den Mittelwert zwischen der Ausgangstemperatur $f (0)$ und $25^{\circ} C$ annimmt.
Dieser Zeitpunkt beträgt etwa $49,5$ Minuten nach der Entnahme aus dem Kühlschrank.
Berechnet wird mit $f (t) = \frac{f (0) + 25}{2}$ ein Mittelwert.
Aus welchen zwei Werten wird der Mittelwert gebildet?
25
Bei einem Glücksspielautomaten gewinnt man, wenn die gleichen
Symbole in der gleichen Farbe angezeigt werden.
Die Wahrscheinlichkeit zu gewinnen, ist bestimmt $\frac{1}{4}$ .
Eine der folgenden Aussagen ist richtig. Kreuze an.
/1P.
Weil es vier Möglichkeiten gibt zu gewinnen, muss es $16$
Möglichkeiten insgesamt geben, denn $4^{2} = 16$ .
Die Wahrscheinlichkeit zu gewinnen ist $\frac{1}{4}$ , wenn insgesamt viermal gedreht wird.
Die Wahrscheinlichkeit zu gewinnen ist $\frac{1}{4}$ , weil das Spiel sonst nicht fair ist.

Oke soll aus den gegebenen Karten eine ziehen.
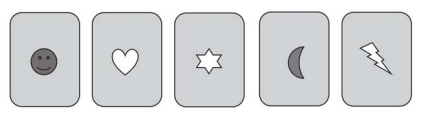
Formuliere eine Spielregel für das Ziehen einer Karte, so dass die
Gewinnchance größer als $\frac{1}{4}$ ist.
/1P.
26
Aufgabe 1
Gegeben ist eine in $ℝ$ definierte Funktion $f (x) = x^{4} - k \cdot x^{2}$ , wobei $k$ eine positive reelle Zahl ist. Abbildung 1 zeigt den Graphen von $f$ .
Abbildung 1
Zeigen Sie, dass $f^{'} (x) = 2 x \cdot (2 x^{2} - k)$ eine Gleichung der ersten Ableitungsfunktion von $f$ ist.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Zeige, dass $f^{'} (x) = 2 x \cdot (2 x^{2} - k)$ eine Gleichung der ersten Ableitungsfunktion von $f$ ist
Gegeben ist $f (x) = x^{4} - k \cdot x^{2}$ .
Dann ist $f^{'} (x) = 4 \cdot x^{3} - 2 \cdot k \cdot x = 2 x \cdot (2 x^{2} - k)$
Leite $f (x)$ ab.

Die beiden Tiefpunkte des Graphen von $f$ haben jeweils die y-Koordinate $- 1$ .
Ermitteln Sie den Wert von $k$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremum
Ermittele den Wert von $k$
Es ist $f^{'} (x) = 2 x \cdot (2 x^{2} - k)$ .
Die notwendige Bedingung für ein Extremum lautet $f^{'} (x) = 0$ .
$\Rightarrow 0 = 2 x \cdot (2 x^{2} - k)$
Mit dem Satz vom Nullprodukt folgt:
$x = 0 \lor x = \pm \sqrt{\frac{k}{2}}$
Die beiden Tiefpunkte des Graphen von $f$ haben jeweils die y-Koordinate $- 1$ .
Zu den beiden Tiefpunkte gehören die Extremstellen $x = \pm \sqrt{\frac{k}{2}}$ .
Für $k > 0$ gilt: $f (\sqrt{\frac{k}{2}}) = - 1 \Rightarrow {(\sqrt{\frac{k}{2}})}^{4} - k \cdot {(\sqrt{\frac{k}{2}})}^{2} = - 1$
$\Rightarrow \frac{k^{2}}{4} - \frac{k^{2}}{2} = - 1 \Rightarrow - \frac{k^{2}}{4} = - 1 \Rightarrow k^{2} = 4 \Rightarrow k = 2$ .
Der gesuchte Wert von $k$ ist $k = 2$ .
Die notwendige Bedingung für ein Extremum lautet $f^{'} (x) = 0$ .
Bestimme die Extremstellen $x_{E}$ .
Die Tiefpunkte liegen nicht bei $x = 0$ .
Löse die Gleichung $f (x_{E}) = - 1$ nach $k$ auf. Beachte $k > 0$ .
27
Aufgabe 2
Die Funktion $f$ ist gegeben durch $f (x) = - x^{3} + 9 x^{2} - 23 x + 15, x \in ℝ$ .
Der Graph von $f$ ist in Abbildung 2 dargestellt.
Abbildung 2
Interpretieren Sie die Aussage $F (5) - F (1) = 0$ in Bezug auf den Graphen von $f$ .
(2 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
Interpretiere die Aussage $F (5) - F (1) = 0$ in Bezug auf den Graphen von $f$
Die Fläche, die im Intervall $[1; 3]$ vom Graphen von $f$ und der x-Achse eingeschlossen wird, ist genauso groß wie die Fläche, die im Intervall $[3; 5]$ vom Graphen von $f$ und der x-Achse eingeschlossen wird
Betrachte die Flächen unterhalb und oberhalb der x-Achse.

Berechnen Sie $\int_{0}^{1} f (x) d x$ . (3 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion
Berechne $\int_{0}^{1} f (x) d x$
Es ist $f (x) = - x^{3} + 9 x^{2} - 23 x + 15$ .
Dann ist $F (x) = - \frac{1}{4} x^{4} + 3 x^{3} - \frac{23}{2} x + 15 x$ eine Stammfunktion von $f$ .
$\int_{0}^{1} f (x) d x = F (1) - F (0) = (- \frac{1}{4} + 3 - \frac{23}{2} + 15) - (0) = 18 - \frac{47}{4} = \frac{25}{4}$
Ergebnis: $\int_{0}^{1} f (x) d x = \frac{25}{4}$ .
Ermittele eine Stammfunktion von $f$ .
Berechne $\int_{0}^{1} f (x) d x = F (1) - F (0)$ .

Begründe, dass $x = 1$ die einzige Nullstelle von $f$ ist

Gegeben ist $f (x) = 10 \cdot (x - 1) \cdot e^{- x}$ .

Für die Nullstellen löse die Gleichung $f (x) = 0$ .

$0 = 10 \cdot (x - 1) \cdot e^{- x}$

Weil $e^{- x} \neq 0$ für alle $x \in ℝ$ folgt mit dem Satz vom Nullprodukt:

$\Rightarrow x - 1 = 0 \Rightarrow x = 1$

Demnach ist $x = 1$ die einzige Nullstelle.

Untersuche $f$ rechnerisch auf lokale Extremstellen
Die notwendige Bedingung für ein Extremum ist $f^{'} (x) = 0$ .
Bilde mithilfe der Produkt- und Kettenregel die 1. Ableitung:
$f^{'} (x) = 10 \cdot (1 \cdot e^{- x} + (x - 1) \cdot e^{- x} \cdot (- 1)) = 10 \cdot (2 - x) \cdot e^{- x}$
$f^{'} (x) = 0 \Rightarrow 0 = 10 \cdot (2 - x) \cdot e^{- x}$
Weil $e^{- x} \neq 0$ für alle $x \in ℝ$ folgt mit dem Satz vom Nullprodukt:
$2 - x = 0 \Rightarrow x = 2$
Die hinreichende Bedingung für ein Extremum ist $f^{''} (x) \neq 0$ .
Bilde mithilfe der Produkt- und Kettenregel die 2. Ableitung:
$f^{''} (x) = 10 \cdot ((- 1) \cdot e^{- x} + (2 - x) \cdot e^{- x} \cdot (- 1)) = 10 \cdot (x - 3) \cdot e^{- x}$
$f^{''} (2) = 10 \cdot (2 - 3) \cdot e^{- 2} = - 10 \cdot e^{- 2} < 0$
Die Funktion $f$ hat genau eine lokale Extremstelle.
Der Graph von $f$ hat bei $x = 2$ ein lokales Maximum.
Zeige rechnerisch, dass der Punkt $(12 | 2160)$ ein Hochpunkt des Graphen von $f$ ist
Gegeben ist $f (x) = - \frac{5}{16} x^{4} + 5 x^{3}$ .
Berechne $f^{'} (x)$ und $f^{''} (x)$ :
$f^{'} (x) = - \frac{5}{4} x^{3} + 15 x^{2}$
$f^{''} (x) = - \frac{15}{4} x^{2} + 30 x$
Die notwendige Bedingung für ein Extremum ist $f^{'} (x) = 0$ .
$\Rightarrow 0 = - \frac{5}{4} x^{3} + 15 x^{2} = 5 x^{2} \cdot (- \frac{1}{4} x + 3)$
Mit dem Satz vom Nullprodukt folgt:
$x = 0 \lor - \frac{1}{4} x + 3 = 0 \Rightarrow x = 12$
Lokale Extremstellen sind also $x = 0$ oder $x = 12$ .
Nach Aufgabenstellung muss nur $x = 12$ beachtet werden.
Die hinreichende Bedingung für ein Extremum ist $f^{''} (x) \neq 0$ .
$\Rightarrow f^{''} (12) = - \frac{15}{4} \cdot 12^{2} + 30 \cdot 12 = - 180 < 0 \Rightarrow$ Maximum
Berechne $f (12) = - \frac{5}{16} \cdot 12^{4} + 5 \cdot 12^{3} = 2160$ .
Der Punkt $(12 | 2160)$ ist ein Hochpunkt des Graphen von $f$ .
Zeige rechnerisch, dass die Tangente an den Graphen von $f$ im Punkt $(0 | 0)$ parallel zur $x$ -Achse verläuft
Es ist $f^{'} (0) = 0$ und $f (0) = 0$ .
Im Punkt $(0 | 0)$ verläuft die Tangente an den Graphen von $f$ parallel zur $x$ -Achse.
Bestimme eine Gleichung der Geraden $g$ , die durch die beiden Wendepunkte des Graphen von $f$ verläuft
Berechne die Wendepunkte:
Die notwendige Bedingung für einen Wendepunkt ist $f^{''} (x) = 0$ .
$\Rightarrow 0 = - \frac{15}{4} x^{2} + 30 x = 15 \cdot x (- \frac{1}{4} \cdot x + 2)$
Mit dem Satz vom Nullprodukt folgt:
$x = 0 \lor - \frac{1}{4} x + 2 = 0 \Rightarrow x = 8$
Wendestellen liegen bei $x = 0$ oder $x = 8$ vor, wenn die hinreichende Bedingung $f^{'''} (x) \neq 0$ erfüllt ist.
Berechne $f^{'''} (x) = - \frac{15}{2} x + 30 \Rightarrow f^{''} (0) = 30 \neq 0$ und $f^{'''} (8) = - \frac{15}{2} \cdot 8 + 30 = - 30 \neq 0$
Die Bedingung ist erfüllt, d.h. Wendestellen liegen bei $x = 0$ oder $x = 8$ vor.
Berechne $f (0) = 0$ und $f (8) = - \frac{5}{16} \cdot 8^{4} + 5 \cdot 8^{3} = 1280$ .
Die Wendepunkte haben die Koordinaten $W P_{1} (0 | 0)$ und $W P_{2} (8 | 1280)$ .
Für die Geradengleichung $g$ benutze die Zwei-Punkte-Form der Geradengleichung:
$y = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \cdot (x - x_{1}) + y_{1} \Rightarrow y = \frac{1280 - 0}{8 - 0} \cdot (x - 0) + 0$
$\Rightarrow g : y = 160 \cdot x$
Die Gleichung der Geraden $g$ , die durch die beiden Wendepunkte des Graphen von $f$ verläuft, lautet $y = 160 \cdot x$ .
Zeichne in die Abbildung eine Gerade ein, die parallel zu $g$ ist und für $0 \leq x \leq 8$ mit dem Graphen von $f$ genau einen Punkt gemeinsam hat
Berechne alle Schnittpunkte des Graphen $G_{f}$ mit den Koordinatenachsen
Gegeben ist $f (x) = \frac{1}{10} (- x^{3} + 15 x^{2} - 56 x + 12)$ .
Schnittpunkte mit der x-Achse:
$f (x) = 0 \Rightarrow \frac{1}{10} (- x^{3} + 15 x^{2} - 56 x + 12) = 0 \Rightarrow - x^{3} + 15 x^{2} - 56 x + 12 = 0$
Die Nullstelle der Funktion $g (x) = - x^{3} + 15 x^{2} - 56 x + 12$ ist bekannt $x_{N} = 6$ .
Führe eine Polynomdivision durch.
$\begin{array}{l} (- x^{3} + 15 x^{2} - 56 x + 12) : (x - 6) = - x^{2} + 9 x - 2 \\ - (- x^{3} + 6 x^{2}) \\ 9 x^{2} - 56 x \\ - (9 x^{2} - 54 x) \\ - 2 x + 12 \\ - (- 2 x + 12) \\ 0 \end{array}$
Löse nun die Gleichung $- x^{2} + 9 x - 2 = 0 \Rightarrow x^{2} - 9 x + 2 = 0$ mit der pq-Formel:
$x_{2,3} =$ $=$ $- \frac{p}{2} \pm \sqrt{{(\frac{p}{2})}^{2} - q}$
↓
Setze $p = - 9$ und $q = 2$ ein.
$=$ $- \frac{(- 9)}{2} \pm \sqrt{{(\frac{- 9}{2})}^{2} - 2}$
$=$ $4,5 \pm \sqrt{20,25 - 2}$
$=$ $4,5 \pm \sqrt{18,25}$
Somit lauten die Schnittpunkte von $G_{f}$ mit der x-Achse $N_{1} (6 | 0), N_{2} (4,5 - \sqrt{18,25} | 0) \approx$ $N_{2} (0,23 | 0)$ und $N_{3} (4,5 + \sqrt{18,25} | 0) \approx N_{3} (8,77 | 0)$ .
Schnittpunkt mit der y-Achse:
Setze $x = 0$ in $f (x)$ ein $\Rightarrow f (0) = 12 \Rightarrow S_{y} (0 | 12)$ .
Der Schnittpunkt mit der y-Achse ist $S_{y} (0 | 12)$ .

Ermittle Art und Koordinaten aller relativen Extrempunkte von $G_{f}$

Gegeben ist die Funktion $h : x \mapsto \arctan (1 - x)^{2}$ in der Definitionsmenge $D_{h} = ℝ$ . Ihr Graph wird mit $G_{h}$ bezeichnet.
a) Legen Sie jeweils mittels aussagekräftiger Rechnung für die Aussagen A, B und C dar, weshalb diese falsch sind:
A: „Der Graph $G_{h}$ ist punktsymmetrisch zum Koordinatenursprung.“
B: „Der Graph $G_{h}$ weist den Tiefpunkt $T (0 | \frac{π}{4})$ auf.“
C: „Für die Wertemenge der Funktion $h$ gilt $W_{h} =] - 2; \frac{π}{4}]$ . “
b) Zeichnen Sie den Graphen G_h der Funktion h unter Verwendung der Erkenntnisse aus Teilaufgabe a) und weiterer geeigneter Funktionswerte für $- 3 \leq x \leq 3$ in ein kartesisches Koordinatensystem.
c) Die Funktion $g$ mit $g (x) = h (x)$ und $D_{g} = [0; 2]$ ist umkehrbar (Nachweis nicht erforderlich). Ihre Umkehrfunktion wird mit $g^{- 1}$ bezeichnet. Ermitteln Sie eine mögliche Funktionsgleichung von $g^{- 1}$ . Bestimmen Sie außerdem die Definitionsmenge und die Wertemenge von $g^{- 1}$ .
3.0 Eine spezielle Rakete mit der Masse m=500 Tonnen befindet sich in Ruhe in einem Bezugssystem, in welchem sie keine Kraft von einem anderen Körper erfährt. Ab dem Zeitpunkt t=0 wird die Rakete nach dem Rückstoßprinzip in Flugrichtung beschleunigt, indem kontinuierlich ein Teil ihrer Masse in Form von Treibstoff mit einer Ausströmgeschwindigkeit $4,0 \frac{k m}{s}$ relativ zur Rakete nach hinten ausgestoßen wird. Folglich hängt die Geschwindigkeit $u$ der Rakete von der abnehmenden Masse $m$ der Rakete ab und kann also durch einen Term $u (m)$ beschrieben werden.
Unter Berücksichtigung, dass $m$ in Tonnen, $u (m)$ in Kilometern pro Sekunde und $t$ in
Sekunden gemessen wird, wird im Folgenden auf das Mitführen der Einheiten verzichtet.
a) Aus dem Impulserhaltungssatz kann man die Differenzialgleichung $m \cdot u^{'} (m) = - 4$ folgern.
Ermitteln Sie die spezielle Lösung dieser Differenzialgleichung für das vorliegende
Anfangswertproblem.
$[Mögliches Ergebnis : u (m) = 4 \cdot \ln (\frac{500}{m})]$
b) Die Masse $m$ der Rakete hängt von der Beschleunigungszeit $t$ ab und wird deshalb durch den Term $m (t)$ beschrieben. Während der ersten $900$ Sekunden nimmt die Masse der Rakete pro Sekunde um $0,5$ Tonnen ab, also gilt:
$m (t) = 500 - 0,5 \cdot t$ für $0 \leq t \leq 900$ .
Die Geschwindigkeit der Rakete in Abhängigkeit von der Zeit $t$ wird mit $v (t)$ bezeichnet, wobei für die ersten $900$ Sekunden gilt: $v (t) = u (m (t))$ .
c) Zeigen Sie, dass gilt: $v (t) = - 4 \cdot \ln (1 - 0,001 \cdot t)$ . Ermitteln Sie zudem den Zeitpunkt $t_{1}$ , zu dem die Rakete eine Geschwindigkeit von $8 \frac{k m}{s}$ hat. Runden Sie Ihr Ergebnis auf eine ganze Zahl.
d) Berechnen Sie das Integral $\int_{0}^{900} v (t) d t$ aus Teilaufgabe c) z. B. mithilfe einer
geeigneten Substitution. Runden Sie Ihr Ergebnis auf eine ganze Zahl und interpretieren Sie das Ergebnis im Sachzusammenhang
Gegeben ist die Funktion $h : x \mapsto \frac{4 + 4 \cdot \ln (x + 1)}{x + 1}$ mit der Definitionsmenge $D_{h} =] - 1; + \infty [$ .
a) Berechnen Sie die Nullstelle von $h$ . Bestimmen Sie außerdem das Verhalten der
Funktionswerte $h (x)$ für $x \to - 1$ .
b) Ermitteln Sie die Wertemenge von $h$ .
$[Mögliches Teilergebnis : h^{'} (x) = \frac{- 4 \cdot \ln (x + 1)}{(x + 1)^{2}}]$
c) Gegeben ist nun die Funktion $H : x \mapsto \int_{0}^{x} h (t) d t$ mit der Definitionsmenge $D_{H} = D_{h}$ .
Bestimmen Sie eine integralfreie Darstellung von $H (x)$ .
Hinweis: Die Substitution $z = \ln (t + 1)$ kann hilfreich sein.
Die Funktion $S$ sei eine Stammfunktion von $H$ mit der Definitionsmenge $D_{S} = D_{H}$ .
Begründen Sie, dass der Graph von $S$ einen Extrempunkt bei $x = 0$ besitzt.
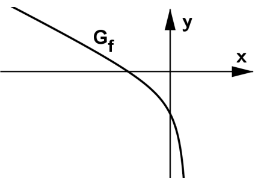
neue Aufgabe 2
Nun wird die Funktion $f : x \mapsto \frac{x^{2} - 1}{1 - 2 x}$ mit der Definitionsmenge $D_{f} =] - \infty; 0,5 [$ betrachtet. Ein Ausschnitt des Graphen von $f$ ist nebenstehend abgebildet.
a) Die Funktion $f$ ist umkehrbar (Nachweis ist nicht erforderlich). Ermitteln Sie eine Gleichung der Umkehrfunktion von $f$ .
b) Zeigen Sie, dass gilt: $f (x) = - \frac{1}{2} x - \frac{1}{4} - \frac{3}{4 \cdot (- 2 x + 1)}$
c) Der Graph von $f$ schließt zusammen mit den beiden Koordinatenachsen im
III. Quadranten des Koordinatensystems ein endliches Flächenstück ein. Ermitteln Sie die Maßzahl des Flächeninhalts dieses Flächenstücks.
neue Aufgabe 3
Bei der Erforschung von speziellen Zellen haben Untersuchungen gezeigt, dass sich das Zellvolumen $V (t)$ (in ${mm}^{3}$ ) in Abhängigkeit von der seit Beobachtungsbeginn $(t = 0)$ verstrichenen Zeit t (in Tagen) mit der Differenzialgleichung $\dot{V} (t) = 0,5 \cdot e^{- 0,2 \cdot t} \cdot V (t)$ beschreiben lässt.
Auf das Mitführen von Einheiten kann in den Rechnungen verzichtet werden.
a) Zeigen Sie, dass die Funktion $V$ mit der Gleichung $V (t) = k \cdot e^{2,5 \cdot (1 - e^{- 0,2 \cdot t})}$ für beliebige Werte von $k \in ℝ^{+}$ eine Lösung der obigen Differenzialgleichung ist. Erläutern Sie außerdem die Bedeutung des Parameters $k$ im Sachzusammenhang.
b) Berechnen Sie unter Verwendung von $V (t)$ aus Teilaufgabe a), auf das Wievielfache das Volumen der Zellen auf lange Sicht anwächst, und ermitteln Sie den Zeitpunkt (auf $2$ Nachkommastellen gerundet), zu dem sich das Volumen der Zellen verdoppelt hat.
Teil 2: mit Hilfsmitteln – Stochastik I 2023
Im Folgenden werden relative Häufigkeiten als Wahrscheinlichkeiten interpretiert.
1.0 Bei einem Hersteller von Elektroautos (E-Autos) können die Kunden beim Kauf eines Autos zwischen den Modellen $A, B$ und $C$ wählen. $30 %$ der Kunden entscheiden sich für Modell $C$ . Die restlichen Kunden wählen zu gleichen Teilen $A$ bzw. $B$ .
Die Modelle $B$ und $C$ werden mit einer kleinen $(K)$ oder einer großen $(G)$ Batterie
angeboten. Das Modell $A$ kann nur mit einer kleinen Batterie bestellt werden. Bei
Modell $B$ entscheiden sich vier von zehn Kunden für die große Batterie, während sich beim Modell $C$ nur $15 %$ der Kunden für die kleine Batterie entscheiden.
Zusätzlich können alle Modelle noch mit einem Autopilot $(P)$ ausgestattet werden. Bei
Modell $B$ und $C$ erfolgt die Wahl unabhängig von der Batteriegröße. Dieses Zusatzangebot wählen beim Modell $A$ $20 %$ der Kunden und beim Modell $B$ jeweils $30 %$ . Insgesamt werden $41,5 %$ aller Fahrzeuge mit Autopilot gewünscht.
Die Wahl des Modells, der Batteriegröße und der Zusatzfunktion Autopilot eines beliebig herausgegriffenen Kunden wird als Zufallsexperiment aufgefasst.
a) Bestimmen Sie unter Verwendung eines Baumdiagramms die Wahrscheinlichkeiten aller zehn Elementarereignisse des betrachteten Zufallsexperiments.
$[$ Teilergebnis: $P ({(C; K; P)}) = 0,036]$
b) Gegeben sind folgende Ereignisse:
$E_{1}$ : „Ein zufällig ausgewählter Kunde wählt Modell $A$ oder $C$ jeweils mit Autopilot.“
$E_{2}$ : „Ein zufällig ausgewählter Kunde wählt entweder die kleine Batterie oder den
Autopilot.“
Berechnen Sie nachvollziehbar jeweils die Wahrscheinlichkeit für $E_{1}$ und für $E_{2}$ .
neue Aufgabe 2
In einer Kleinstadt sind $30 %$ aller zugelassenen Elektroautos der Oberklasse $(O)$
zuzuordnen, die restlichen werden der Mittelklasse $(M)$ zugeordnet. Die Akkus aller hier betrachteten Elektroautos werden zu $39,5 %$ regelmäßig über eine Photovoltaik-Anlage $(V)$ des jeweiligen Fahrzeugeigners geladen. Die Wahrscheinlichkeit dafür, dass ein zufällig aus all diesen Fahrzeugen ausgewähltes Elektroauto ein Modell der Oberklasse ist und regelmäßig über eine Photovoltaik-Anlage aufgeladen wird, beträgt $25,5 %$ .
a) Erstellen Sie eine vollständig ausgefüllte Vierfeldertafel und berechnen Sie die
Wahrscheinlichkeit des Ereignisses $E_{3} = M \cap V$ .
b) Untersuchen Sie, ob der Anteil der Fahrzeuge, die über eine Photovoltaik-Anlage des Fahrzeugeigners geladen werden, bei den Oberklasse-Modellen höher ist als bei den Mittelklasse-Modellen. Entscheiden Sie anschließend, ob die Ereignisse $M$ und $V$ stochastisch unabhängig sind.
Neue Aufgabe
T13 – Teil 2: mit Hilfsmitteln – Stochastik I (Fortsetzung) 2023
Am Parkplatz eines großen Einkaufszentrums wurde im Rahmen einer Bachelor-Arbeit eine lang angelegte Studie zum Laden von E-Autos an den dort vorhandenen Ladesäulen durchgeführt. Diese lieferte folgende Ergebnisse: $80 %$ der Ladevorgänge erfolgen während der Zeit, in der die Besitzer der Fahrzeuge im Einkaufszentrum verweilen. Alle anderen Besitzer verbringen die Ladezeit in den umliegenden kleineren Geschäften, Bars, Cafés oder im Biergarten. Zudem wurde festgestellt, dass $5 %$ aller auf dem Parkplatz parkenden Pkw E-Autos sind.
Bestimmen Sie, basierend auf den Ergebnissen der Studie, die Wahrscheinlichkeiten der folgenden Ereignisse:
$E_{4}$ : „Unter elf Ladevorgängen erfolgen genau neun in der Zeit, in der die Besitzer der
Fahrzeuge im Einkaufszentrum verweilen.“
$E_{5}$ : „Unter $50$ Ladevorgängen erfolgen mehr als neun, aber weniger als $18$ in der Zeit, in der die Besitzer der Fahrzeuge nicht im Einkaufszentrum verweilen.“
$E_{6}$ : „Unter $100$ auf dem Parkplatz parkenden Pkw sind mehr E-Autos als nach der Studie zu erwarten wären.“
T13 – Teil 2: mit Hilfsmitteln – Stochastik II 2023
Im Folgenden werden relative Häufigkeiten als Wahrscheinlichkeiten interpretiert.
Am Pausenverkauf einer großen Mädchenschule kaufen an einem Tag erfahrungsgemäß $30 %$ aller Schülerinnen eine Breze. Es werden 20 Schülerinnen an einem bestimmten Tag zufällig ausgewählt. Die Zufallsgröße $X$ gibt an, wie viele von diesen am betrachteten Tag eine Breze kaufen.
a) Berechnen Sie die Wahrscheinlichkeiten der folgenden Ereignisse:
$E_{1}$ : „Nur die letzten beiden Schülerinnen kaufen eine Breze.“
$E_{2}$ : „Genau zehn der Schülerinnen kaufen keine Breze.“
b) Berechnen Sie den Erwartungswert der Zufallsgröße $X$ und interpretieren Sie diesen im Sachzusammenhang.
c) Bestimmen Sie die Wahrscheinlichkeit, mit der die Zufallswerte von $X$ innerhalb der einfachen Standardabweichung um den Erwartungswert liegen.
d) Berechnen Sie die Wahrscheinlichkeit des Ereignisses:
$E_{3}$ : „Mehr als doppelt so viele Schülerinnen wie erwartet kaufen eine Breze.“
neue Aufgabe 2
In einer Urne befinden sich sechs grüne, eine rote und eine blaue Kugel. Ein
Zufallsexperiment besteht darin, nacheinander jeweils zufällig eine Kugel ohne
Zurücklegen zu ziehen und deren Farbe festzustellen. Es wird so lange gezogen, bis die blaue Kugel erscheint, höchstens jedoch dreimal.
a) Bestimmen Sie unter Verwendung eines Baumdiagramms die Wahrscheinlichkeiten aller zehn Elementarereignisse des betrachteten Zufallsexperiments.
b) Es werden nun folgende Ereignisse betrachtet:
$A$ : „Es werden alle drei Farben gezogen.“
$B$ : „Das Zufallsexperiment endet mit der blauen Kugel.“
Berechnen Sie nachvollziehbar die Wahrscheinlichkeiten für die Ereignisse $A$ und $B$ .
$[$ Teilergebnis: $P (B) = \frac{3}{8}]$
c) Bestimmen Sie die Wahrscheinlichkeit dafür, dass insgesamt drei Kugeln gezogen werden unter der Bedingung, dass das Zufallsexperiment mit der blauen Kugel endet.

29
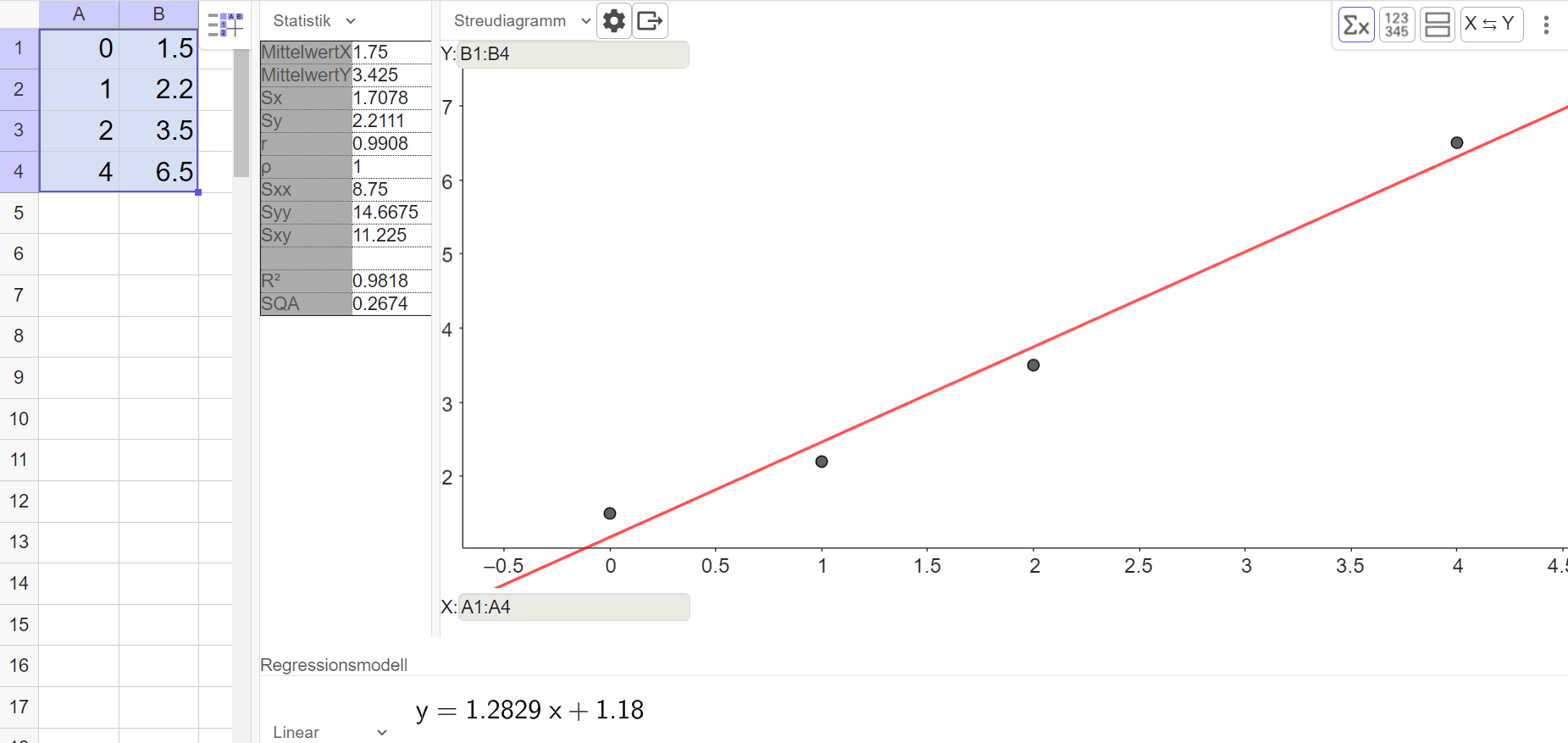
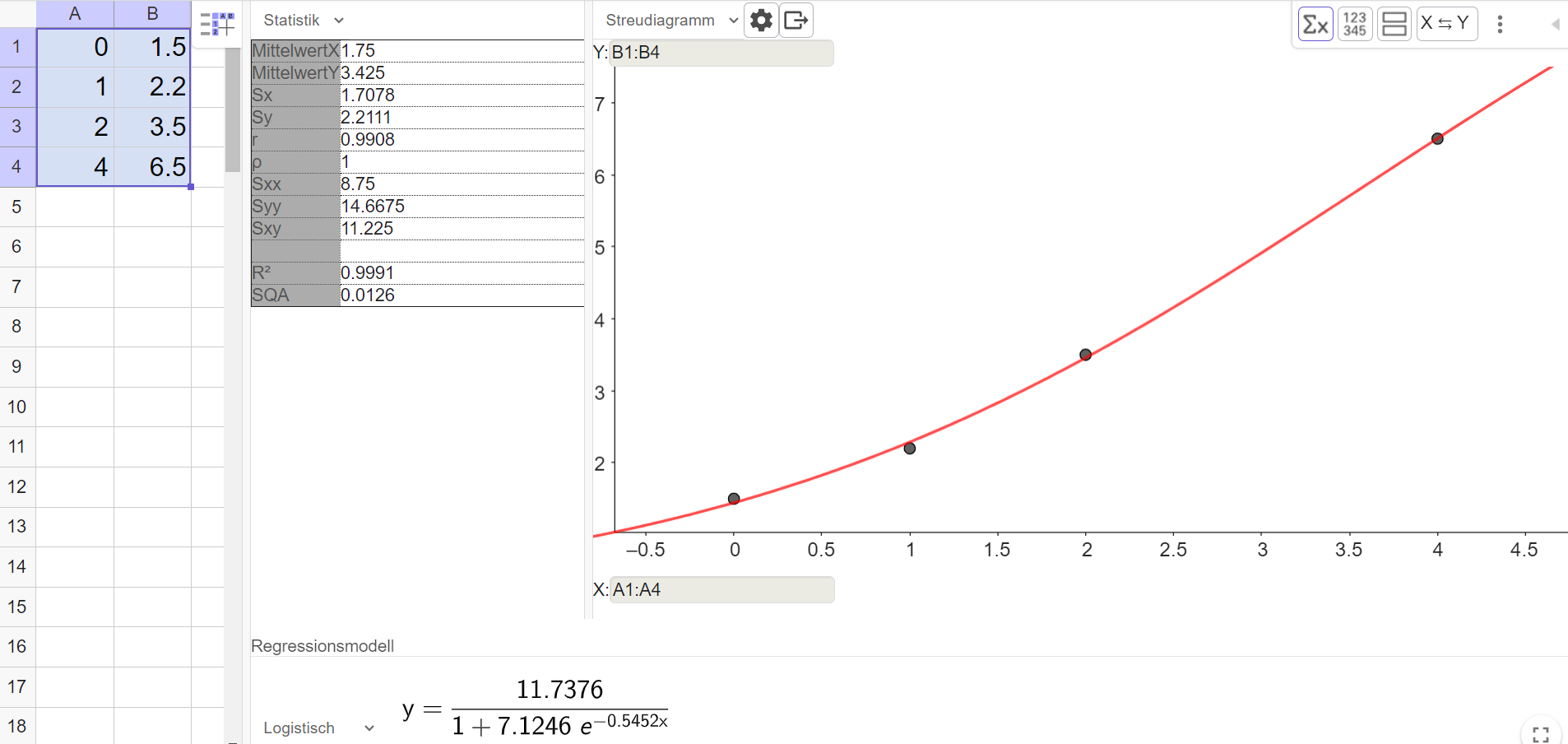
Herr Malinowski sieht auf seiner App der Gasverbrauch pro Tag in $m^{3}$ innerhalb einer Woche.
Er denkt darüber nach, welche mathematische Funktion den Gasverbrauch beschreiben kann und vermutet, dass es sich um eine e-Funktion handeln könnte.
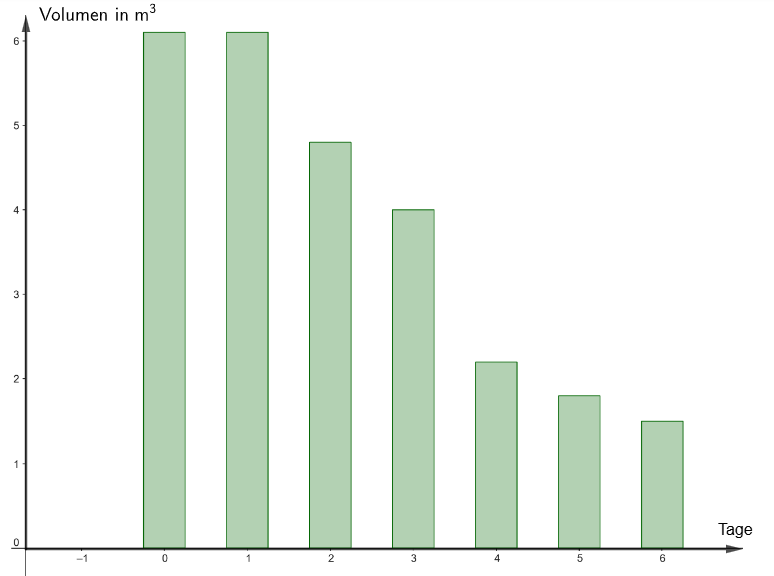
Abbildung
Die zur Abbildung gehörenden Daten findest Du in der folgenden Tabelle.
x in
Tagen
y in
$m^{3}$
0
6,1
1
6,1
2
4,8
3
4
4
2,2
5
1,8
6
1,5
Erstelle mit dem TR oder mit Geogebra eine Regressionsfunktion mit dem Ansatz $f (x) = A \cdot e^{B x}$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Regression
Man erhält als Ergebnis die Funktion $f (x) = 7,311 \cdot e^{- 0,265 x}$ .
$r = - 0,9722, r^{2} = 0,9452, M S e = 0,02286$
Die folgende Abbildung veranschaulicht das Ergebnis.
Regressionsfunktion

Herr Malinowski zeigt das Ergebnis seiner Analyse seinem Nachbarn. Der ist der Meinung, dass auch andere Regressionsfunktionen zu den Daten passen würden.
Überprüfe mit dem TR oder mit Geogebra, welche Regressionsfunktionen auch möglich sind. Was ist die beste Regressionsfunktion?

Lineare Regression:
$f (x) = - 0,8929 x + 6,4643$
$r = - 0,97525, r^{2} = 0,95112, M S e = 0,22943$
Polynom 3. Grades:
$f (x) = 0,0639 x^{3} - 0,5631 x^{2} + 0,3135 x + 6,1405$
$r^{2} = 0,98919, M S e = 0,08452$
Trigonometrische Funktion:
$f (x) = 2,34111 \cdot \sin (0,58622 x + 1,42514) + 3,8290$
$r^{2} = 0,9894,$ $M S e = 0,04999$
Logistische Regression:
Hier gibt es zwei unterschiedliche Ergebnisse.
$f (x) = \frac{- 18,73187}{1 - 3,75786 \cdot e^{0,19445 x}}$ , $M S e = 0,4965$
$f (x) = \frac{7,3619}{1 + 0,1574 \cdot e^{0,5952 x}}, r^{2} = 0,9713$
Ergebnis:
Die beste Regression liefert die Sinus-Funktion.

x in Tagen	y in $m^{3}$
0	6,1
1	6,1
2	4,8
3	4
4	2,2
5	1,8
6	1,5

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org

$s^{2} - t_{2}^{2}$	$=$	$r^{2} - t_{1}^{2}$
	↓	Setze $t_{2} = t - t_{1}$ ein.
$s^{2} - (t - t_{1})^{2}$	$=$	$r^{2} - t_{1}^{2}$
	↓	Löse die Klammer auf, verwende eine binomische Formel.
$s^{2} - (t^{2} - 2 \cdot t \cdot t_{1} + t_{1}^{2})$	$=$	$r^{2} - t_{1}^{2}$
	↓	Löse die Klammer auf.
$s^{2} - t^{2} + 2 \cdot t \cdot t_{1} - t_{1}^{2}$	$=$	$r^{2} - t_{1}^{2}$	$+ t_{1}^{2}$
	↓	Löse nach $t_{1}$ auf.
$s^{2} - t^{2} + 2 \cdot t \cdot t_{1}$	$=$	$r^{2}$	$- s^{2}$
$- t^{2} + 2 \cdot t \cdot t_{1}$	$=$	$r^{2} - s^{2}$	$+ t^{2}$
$2 \cdot t \cdot t_{1}$	$=$	$r^{2} - s^{2} + t^{2}$	$: 2 t$
$t_{1}$	$=$	$\frac{r^{2} - s^{2} + t^{2}}{2 t}$

$A_{1}^{2} + A_{2}^{2} + A_{3}^{2}$	$=$	$A_{4}^{2}$
	↓	Setze die berechneten Werte ein.
$(24 {cm}^{2})^{2} + (12 {cm}^{2})^{2} + (16 {cm}^{2})^{2}$	$=$	$(\sqrt{976} {cm}^{2})^{2}$
$576 {cm}^{4} + 144 {cm}^{4} + 256 {cm}^{4}$	$=$	$976 {cm}^{4}$
$976 {cm}^{4}$	$=$	$976 {cm}^{4} ✓$

$a x + b y$	$=$	$c$	$- a x$
	↓	Nach $y$ auflösen.
$b y$	$=$	$- a x + c$	$: b$
$y$	$=$	$- \frac{a}{b} \cdot x + \frac{c}{b}$

$(4 + 2 t) - 3 (t) + 3 (1)$	$=$	$6$
	↓	Löse die Klammern auf
$4 + 2 t - 3 t + 3$	$=$	$6$
	↓	Löse nach $t$ auf.
$7 - t$	$=$	$6$	$- 7$
$- t$	$=$	$- 1$	$\cdot (- 1)$
$t$	$=$	$1$

$\vec{p}^{'} \circ \vec{n}$	$=$	$2 \cdot d - d_{1}$
	↓	Setze $\vec{p}^{'} = \vec{p} + t \cdot \vec{n}$ ein.
$(\vec{p} + t \cdot \vec{n}) \circ \vec{n}$	$=$	$2 \cdot d - d_{1}$
$\vec{p} \circ \vec{n} + t \cdot \vec{n} \circ \vec{n}$	$=$	$= 2 \cdot d - d_{1}$

$\vec{p} \circ \vec{n} + t \cdot \vec{n} \circ \vec{n}$	$=$	$2 \cdot d - d_{1}$
	↓	Setze $\vec{p} \circ \vec{n} = d_{1}$ ein.
$d_{1} + t \cdot \vec{n} \circ \vec{n}$	$=$	$2 \cdot d - d_{1}$	$- d_{1}$
$t \cdot \vec{n} \circ \vec{n}$	$=$	$2 \cdot d - 2 \cdot d_{1}$
$t \cdot \vec{n} \circ \vec{n}$	$=$	$2 \cdot (d - d_{1})$	$: \vec{n} \circ \vec{n}$
$t$	$=$	$\frac{2 \cdot (d - d_{1})}{\vec{n} \circ \vec{n}}$

$x_{1, 2}$	$=$	$\frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$
	↓	Setze $a = 2$ , $b = - 28$ und $ c = 98$ ein.
	$=$	$\frac{- (- 28) \pm \sqrt{(- 28)^{2} - 4 \cdot 2 \cdot 98}}{2 \cdot 2}$
	$=$	$\frac{28 \pm \sqrt{784 - 784}}{4}$
	$=$	$\frac{28 \pm 0}{4}$
	$=$	$7$

$x_{1,2}$	$=$	$\frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$
	↓	Setze $a = - 3$ , $b = - 4$ und $ c = 5$ ein.
	$=$	$\frac{- (- 4) \pm \sqrt{(- 4)^{2} - 4 \cdot (- 3) \cdot 5}}{2 \cdot (- 3)}$
	$=$	$\frac{4 \pm \sqrt{16 + 60}}{(- 6)}$
	$=$	$\frac{4 \pm \sqrt{76}}{(- 6)}$
	$=$	$\frac{4 \pm \sqrt{4 \cdot 19}}{(- 6)}$
	$=$	$\frac{4 \pm 2 \cdot \sqrt{19}}{(- 6)}$
	↓	Klammere $2$ aus und kürze.
	$=$	$- \frac{2 \pm \sqrt{19}}{3}$

$t_{1}$	$=$	$\frac{80 - 52 + 100}{2 \cdot 10}$
$t_{1}$	$=$	$\frac{128}{20}$
$t_{1}$	$=$	$6,4$

		gegeben	gegeben	gegeben $\cot φ$
				$\frac{1}{\pm \sqrt{1 + \cot^{2} φ}}$
				$\frac{\cot φ}{\sqrt{1 + \cot^{2} φ}}$
				$\frac{1}{\cot φ}$
$? ? \cot φ =$	$\frac{\pm \sqrt{1 - \sin^{2} φ}}{\sin φ}$	$\frac{\cos φ}{\pm \sqrt{1 - \cos^{2} φ}}$	$\frac{1}{\tan φ}$	$\cot φ$

$- \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \cdot x_{1} + y_{1} \cdot (x_{2} - x_{1})$	$=$	$\frac{c}{b}$
	↓	Setze $b = x_{2} - x_{1}$ ein.
$- \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \cdot x_{1} + y_{1}$	$=$	$\frac{c}{x_{2} - x_{1}}$	$\cdot (x_{2} - x_{1})$
$(- \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \cdot x_{1} + y_{1}) \cdot (x_{2} - x_{1})$	$=$	$c$
	↓	Multipliziere die Klammer aus.
$- \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \cdot x_{1} \cdot (x_{2} - x_{1}) + y_{1} \cdot (x_{2} - x_{1})$	$=$	$c$
	↓	Kürze.
$- (y_{2} - y_{1}) \cdot x_{1} + y_{1} \cdot (x_{2} - x_{1})$	$=$	$c$
	↓	Löse die Klammern auf.
$- y_{2} \cdot x_{1} + y_{1} \cdot x_{1} + y_{1} \cdot x_{2} - y_{1} \cdot x_{1}$	$=$	$c$
	↓	Fasse zusammen.
$- y_{2} \cdot x_{1} + y_{1} \cdot x_{2}$	$=$	$c$

$f^{'} (x)$	$=$	$(x - \frac{1}{2}) \cdot e^{2 x + 1} + (\frac{1}{2} x^{2} - \frac{1}{2} x - \frac{7}{4}) \cdot 2 \cdot e^{2 x + 1}$
	↓	Klammere $e^{2 x + 1}$ aus. Multipliziere die $2$ in die hintere Klammer.
	$=$	$e^{2 x + 1} (x - \frac{1}{2} + x^{2} - x - \frac{7}{2})$
	↓	Fasse zusammen.
	$=$	$e^{2 x + 1} (x^{2} - 4)$

$x_{2,3} =$	$=$	$- \frac{p}{2} \pm \sqrt{{(\frac{p}{2})}^{2} - q}$
	↓	Setze $p = - 9$ und $q = 2$ ein.
	$=$	$- \frac{(- 9)}{2} \pm \sqrt{{(\frac{- 9}{2})}^{2} - 2}$
	$=$	$4,5 \pm \sqrt{20,25 - 2}$
	$=$	$4,5 \pm \sqrt{18,25}$

$x_{1,2}$	$=$	$\frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$
	↓	Setze $a = - 3, b = 30$ und $c = - 56$ ein.
	$=$	$\frac{- 30 \pm \sqrt{30^{2} - 4 \cdot (- 3) \cdot (- 56)}}{2 \cdot (- 3)}$
	↓	Fasse zusammen.
	$=$	$\frac{- 30 \pm \sqrt{900 - 672}}{2 \cdot (- 3)}$
	$=$	$\frac{- 30 \pm \sqrt{228}}{2 \cdot (- 3)}$
	↓	Schreibe $228$ als $4 \cdot 57$ .
	$=$	$\frac{- 30 \pm \sqrt{4 \cdot 57}}{2 \cdot (- 3)}$
	↓	Ziehe teilweise die Wurzel.
	$=$	$\frac{- 30 \pm 2 \cdot \sqrt{57}}{2 \cdot (- 3)}$
	↓	Klammere im Zähler $2$ aus und kürze.
	$=$	$\frac{- 15 \pm \sqrt{57}}{(- 3)}$
	↓	Klammere im Zähler $(- 1)$ aus und kürze
	$=$	$\frac{15 \mp \sqrt{57}}{3}$

Aufgaben

Vorgehensweise bei der Lagebestimmung

1. Um die Lagebeziehung zwischen einer Geraden und einer Ebene zu bestimmen, ist es empfehlenswert wenn man eine Parametergleichung der Geraden und eine Koordinatengleichung der Ebene verwendet.

2. Die Geradengleichung wird in die Koordinatenform der Ebene eingesetzt.

3. Die Gleichung wird nach der Variablen aufgelöst. Dabei sind verschiedene Ergebnisse möglich, die einen Rückschluss auf die Lagebeziehung zwischen Gerade und Ebene erlauben.

Mögliche Ergebnisse, die bei der Gleichungsauflösung auftreten können:

Im Spoiler findet man Lösungen für andere Formen der Ebenengleichung.

Axialschnitt eines Rotationskörpers

Lösung zu 1

Lösung zu 2

Fallunterscheidung

Lösung zu 3

Fallunterscheidung

limx→−∞⁡(x⋅eax+3a)=limx→−∞⁡x⋅eax⏟→0+3a=3a

Lösung zu 4

Tabelle für f−3(x)=x⋅e−3x−1:

Tabelle für f1=x⋅ex+3:

Darstellung der Graphen von K−3 und von K1.

Lösung zu 5

Lösung zu 6

Schritt 1

Schritt 2

Der Punkt PF wird nun als konstant betrachtet und der Punkt Q ist variabel in Abhängigkeit von s.

Beispiel:

Beispiel

Beispiel 1

Lösung für Beispiel 1

Beispiel 2

Lösung für Beispiel 2

Lösung zu a)

Lösung zu b)

Lösung zu a)

Lösung zu b)

Lösung zu a)

Lösung zu b)

Lösung zu c)

Lösung zu a)

Lösung zu b)

Lösung zu a)

Lösung zu b)

Lösung zu a)

Lösung zu b)

Lageuntersuchung: g∩E

Berechnung des Schnittpunktes der Geraden mit der Ebene

Lösung zu a)

Lösung zu b)

Lageuntersuchung:

Lösung zu a)

Lösung zu b)

Lösung zu a)

Lösung zu b)

Lösung zu c)

Lösung zu a)

Lösung zu b)

Lösung zu a)

Lösung zu b)

Lösung zu a)

Lösung zu b)

Lösung zu a)

Lösung zu b)

Lösung zu a)

Lösung zu b)

Lösung zu a)

Lösung zu b)

Lösung zu c)

Lösung zu d)

Lösung zu e)

Lösung

Lösung zu a)

Nachweis, dass der Spiegel in der Ebene E1 liegt

Spiegeldrehung

Lage der Ebene Et in Abhängigkeit von t

Et:x1+t⋅x2=2⋅t

Lösung zu b)

Lösung zu c)

Geradengleichung für den Lichtstrahl

Fallunterscheidung:

Lösung zu a)

Lösung zu b)

Lösung zu c)

$\lim_{x \to - \infty} (x \cdot e^{a x} + \frac{3}{a}) = \lim_{x \to - \infty} \underset{\to 0}{\underset{⏟}{x \cdot e^{a x}}} + \frac{3}{a} = \frac{3}{a}$

Tabelle für $f_{- 3} (x) = x \cdot e^{- 3 x} - 1$ :

Tabelle für $f_{1} = x \cdot e^{x} + 3$ :

Darstellung der Graphen von $K_{- 3}$ und von $K_{1}$ .

Der Punkt $P_{F}$ wird nun als konstant betrachtet und der Punkt $Q$ ist variabel in Abhängigkeit von $s$ .

Lageuntersuchung: $g \cap E$

Nachweis, dass der Spiegel in der Ebene $E_{1}$ liegt

Lage der Ebene $E_{t}$ in Abhängigkeit von $t$

$E_{t} : x_{1} + t \cdot x_{2} = 2 \cdot t$

Wie wird $d_{3}$ berechnet?

Alternative Berechnung der Spiegelung eines Punktes $P$ an einer Ebene $E$

Geben Sie den Zeitpunkt an, zu dem die Konzentration erstmals den Wert $2,8 \frac{mg}{l}$ annimmt.

Bestimmen Sie, wie lange die Konzentration mindestens $0,5 \frac{mg}{l}$ beträgt.

1. Möglichkeit für den Nachweis der Punktsymmetrie zu $O (0 | 0)$

2. Möglichkeit für den Nachweis der Punktsymmetrie zu $O (0 | 0)$

1. Möglichkeit für den Nachweis der Punktsymmetrie zu $O (0 | 0)$

2. Möglichkeit für den Nachweis der Punktsymmetrie zu $O (0 | 0)$

1. Möglichkeit für den Nachweis der Punktsymmetrie zu $O (0 | 0)$

2. Möglichkeit für den Nachweis der Punktsymmetrie zu $O (0 | 0)$

1. Möglichkeit für den Nachweis der Punktsymmetrie zu $O (0 | 0)$

2. Möglichkeit für den Nachweis der Punktsymmetrie zu $O (0 | 0)$

1. Möglichkeit für den Nachweis der Punktsymmetrie zu $P (- 3 | 4)$

2. Möglichkeit für den Nachweis der Punktsymmetrie zu $P (- 3 | 4)$

Zeige, dass der Graph der Funktion $f$ punktsymmetrisch ist

Für welchen Parameterwert $b$ ergibt sich ein Quadrat?

Zeige, dass $f^{'} (x) = 2 x \cdot (2 x^{2} - k)$ eine Gleichung der ersten Ableitungsfunktion von $f$ ist

Ermittele den Wert von $k$

Interpretiere die Aussage $F (5) - F (1) = 0$ in Bezug auf den Graphen von $f$

Berechne $\int_{0}^{1} f (x) d x$

Begründe, dass $x = 1$ die einzige Nullstelle von $f$ ist

Untersuche $f$ rechnerisch auf lokale Extremstellen

Zeige rechnerisch, dass der Punkt $(12 | 2160)$ ein Hochpunkt des Graphen von $f$ ist

Zeige rechnerisch, dass die Tangente an den Graphen von $f$ im Punkt $(0 | 0)$ parallel zur $x$ -Achse verläuft

Bestimme eine Gleichung der Geraden $g$ , die durch die beiden Wendepunkte des Graphen von $f$ verläuft

Zeichne in die Abbildung eine Gerade ein, die parallel zu $g$ ist und für $0 \leq x \leq 8$ mit dem Graphen von $f$ genau einen Punkt gemeinsam hat

Berechne alle Schnittpunkte des Graphen $G_{f}$ mit den Koordinatenachsen

Ermittle Art und Koordinaten aller relativen Extrempunkte von $G_{f}$

Ermittle Art und Koordinaten aller relativen Extrempunkte von $G_{f}$