Abbildungen im Raum mithilfe von Matrizen (2)

Orthogonale Spiegelung eines Punktes an einer Ebene, die durch den Ursprung verläuft

Gegeben sind ein Punkt $P (a | b | c)$ und eine Ebene $E$ .

Gesucht sind die Koordinaten des Bildpunktes $P^{'}$ bei orthogonaler Spiegelung an der Ebene $E$ .

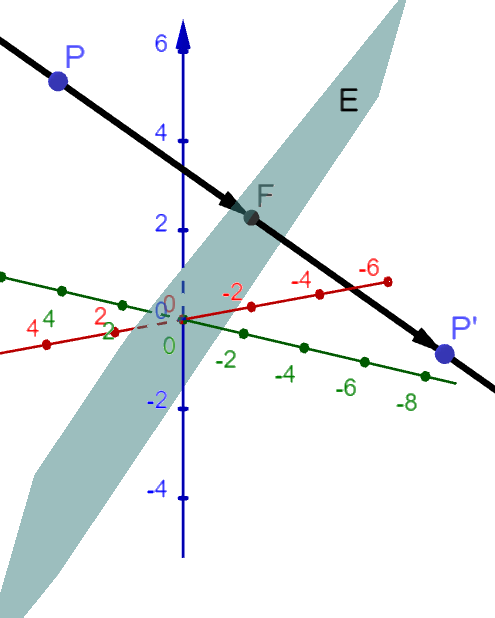
Orthogonale Spiegelung eines Punktes an einer Ebene durch den Ursprung

Der Bildpunkt $P^{'}$ eines beliebigen Punktes $P (a | b | c)$ ist gegeben durch:

$\vec{O P^{'}} = \vec{O P} + 2 \cdot \vec{P F}$

Dabei ist $F$ der Schnittpunkt der Lotgeraden $g_{Lot} : \vec{x} = (\begin{array}{c} a \\ b \\ c \end{array}) + r \cdot (\begin{array}{c} n_{1} \\ n_{2} \\ n_{3} \end{array})$ mit der Ebene $E : n_{1} \cdot x_{1} + n_{2} \cdot x_{2} + n_{3} \cdot x_{3} = 0.$

Der Vektor $(\begin{array}{c} n_{1} \\ n_{2} \\ n_{3} \end{array})$ ist der Normalenvektor der Ebene $E$ .

Schneide $g_{Lot}$ mit $E$ :

$n_{1} \cdot (a + r \cdot n_{1}) + n_{2} \cdot (b + r \cdot n_{2}) + n_{3} \cdot (c + r \cdot n_{3})$	$=$	$0$
	↓	Löse die Klammern auf.
$n_{1} \cdot a + r \cdot n_{1}^{2} + n_{2} \cdot b + r \cdot n_{2}^{2} + n_{3} \cdot c + r \cdot n_{3}^{2}$	$=$	$0$	$- n_{1} \cdot a - n_{2} \cdot b - n_{3} \cdot c$
$r \cdot n_{1}^{2} + r \cdot n_{2}^{2} + r \cdot n_{3}^{2}$	$=$	$- n_{1} \cdot a - n_{2} \cdot b - n_{3} \cdot c$
	↓	Klammere $r$ aus.
$r \cdot (n_{1}^{2} + n_{2}^{2} + n_{3}^{2})$	$=$	$- n_{1} \cdot a - n_{2} \cdot b - n_{3} \cdot c$	$: (n_{1}^{2} + n_{2}^{2} + n_{3}^{2})$
	↓	Löse nach r auf.
$r$	$=$	$- \frac{n_{1} \cdot a + n_{2} \cdot b + n_{3} \cdot c}{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}$

Setze $r$ in $g_{Lot}$ ein:

$\vec{O F} = (\begin{array}{c} a \\ b \\ c \end{array}) - (\frac{n_{1} \cdot a + n_{2} \cdot b + n_{3} \cdot c}{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}) \cdot (\begin{array}{c} n_{1} \\ n_{2} \\ n_{3} \end{array}) = \vec{O P} - (\frac{n_{1} \cdot a + n_{2} \cdot b + n_{3} \cdot c}{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}) \cdot (\begin{array}{c} n_{1} \\ n_{2} \\ n_{3} \end{array})$

$\vec{P F} = \vec{O F} - \vec{O P} = - (\frac{n_{1} \cdot a + n_{2} \cdot b + n_{3} \cdot c}{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}) \cdot (\begin{array}{c} n_{1} \\ n_{2} \\ n_{3} \end{array})$

Setze $\vec{P F}$ in $\vec{O P^{'}} = \vec{O P} + 2 \cdot \vec{P F}$ ein:

$\vec{O P^{'}} = (\begin{array}{c} a \\ b \\ c \end{array}) - 2 \cdot (\frac{n_{1} \cdot a + n_{2} \cdot b + n_{3} \cdot c}{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}) \cdot (\begin{array}{c} n_{1} \\ n_{2} \\ n_{3} \end{array})$

$\vec{O P^{'}} = \frac{1}{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}} (\begin{array}{cc} a \cdot (n_{1}^{2} + n_{2}^{2} + n_{3}^{2}) & - 2 \cdot (n_{1} \cdot a + n_{2} \cdot b + n_{3} \cdot c) \cdot n_{1} \\ b \cdot (n_{1}^{2} + n_{2}^{2} + n_{3}^{2}) & - 2 \cdot (n_{1} \cdot a + n_{2} \cdot b + n_{3} \cdot c) \cdot n_{2} \\ c \cdot (n_{1}^{2} + n_{2}^{2} + n_{3}^{2}) & - 2 \cdot (n_{1} \cdot a + n_{2} \cdot b + n_{3} \cdot c) \cdot n_{3} \end{array})$

$\vec{O P^{'}} = \frac{1}{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}} (\begin{array}{cc} a \cdot n_{1}^{2} + a \cdot n_{2}^{2} + a \cdot n_{3}^{2} & - 2 \cdot n_{1}^{2} \cdot a - 2 \cdot n_{1} \cdot n_{2} \cdot b - 2 \cdot n_{1} \cdot n_{3} \cdot c \\ b \cdot n_{1}^{2} + b \cdot n_{2}^{2} + b \cdot n_{3}^{2} & - 2 \cdot n_{1} \cdot n_{2} \cdot a - 2 \cdot n_{2}^{2} \cdot b - 2 \cdot n_{2} \cdot n_{3} \cdot c \\ c \cdot n_{1}^{2} + c \cdot n_{2}^{2} + c \cdot n_{3}^{2} & - 2 \cdot n_{1} \cdot n_{3} \cdot a - 2 \cdot n_{2} \cdot n_{3} \cdot b - 2 \cdot n_{3}^{2} \cdot c \end{array})$

$\vec{O P^{'}} = \frac{1}{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}} (\begin{array}{ccc} - a \cdot n_{1}^{2} + a \cdot n_{2}^{2} + a \cdot n_{3}^{2} & - 2 n_{1} \cdot n_{2} \cdot b & - 2 \cdot n_{1} \cdot n_{3} \cdot c \\ b \cdot n_{1}^{2} - b \cdot n_{2}^{2} + b \cdot n_{3}^{2} & - 2 \cdot n_{1} \cdot n_{2} \cdot a & - 2 \cdot n_{2} \cdot n_{3} \cdot c \\ c \cdot n_{1}^{2} + c \cdot n_{2}^{2} - c \cdot n_{3}^{2} & - 2 \cdot n_{1} \cdot n_{3} \cdot a & - 2 \cdot n_{2} \cdot n_{3} \cdot b \end{array})$

Zeile $2$ und Zeile $3$ müssen umsortiert werden und $(\begin{array}{c} a \\ b \\ c \end{array})$ wird aus der Klammer herausgezogen:

$\vec{O P^{'}} = \frac{1}{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}} (\begin{array}{ccc} - n_{1}^{2} + n_{2}^{2} + n_{3}^{2} & - 2 n_{1} \cdot n_{2} & - 2 \cdot n_{1} \cdot n_{3} \\ - 2 \cdot n_{1} \cdot n_{2} & n_{1}^{2} - n_{2}^{2} + n_{3}^{2} & - 2 \cdot n_{2} \cdot n_{3} \\ - 2 \cdot n_{1} \cdot n_{3} & - 2 \cdot n_{2} \cdot n_{3} & n_{1}^{2} + n_{2}^{2} - n_{3}^{2} \end{array}) \cdot (\begin{array}{c} a \\ b \\ c \end{array})$

Die Spiegelungsmatrix $S$ lautet also:,

S = \frac{1}{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}} (\begin{array}{ccc} - n_{1}^{2} + n_{2}^{2} + n_{3}^{2} & - 2 n_{1} \cdot n_{2} & - 2 \cdot n_{1} \cdot n_{3} \\ - 2 \cdot n_{1} \cdot n_{2} & n_{1}^{2} - n_{2}^{2} + n_{3}^{2} & - 2 \cdot n_{2} \cdot n_{3} \\ - 2 \cdot n_{1} \cdot n_{3} & - 2 \cdot n_{2} \cdot n_{3} & n_{1}^{2} + n_{2}^{2} - n_{3}^{2} \end{array})

MerkeOrthogonale Spiegelung

Für eine orthogonale Spiegelung an der Ebene $F$ mit der Abbildungsmatrix $S$ gilt:

Jeder Punkt der Ebene $F$ ist ein Fixpunkt, d.h ein Punkt, der bei einer Abbildung auf sich selbst abgebildet wird.
Für jede Spiegelung gilt: $S \cdot S = S^{2} = E$ (dabei ist $E$ die Einheitsmatrix)
Die Spaltenvektoren der Spiegelmatrix haben die Länge $1$ und sind paarweise orthogonal zueinander.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org