Elektromagnetische Induktion Teil 2
In einem vorangegangen Artikel haben wir das Auftreten einer elektrischen Spannung bei geradlinigen Bewegungen von Leitern und Leiterschleifen im Zusammenspiel mit Magnetfeldern beobachten können.
In nachfolgendem Artikel betrachten wir nun die drehende Bewegung einer Leiterschleife im Magnetfeld und das Auftreten einer besonderen Induktionsspannung in Form einer Sinusschwingung.

Exemplarische Darstellung einer Sinuswelle
Wiederholung und Einführung in das Thema
Um die nachfolgenden Ausführungen besser verstehen zu können, raten wir Dir den vorangegangen Artikel ( LINK) kurz zu wiederholen.
Hierin besonders wichtig ist der formale Zusammenhang: wobei gilt
Unser besonderes Augenmerk liegt auf dem Quotienten , welcher die Flächenänderung einer Leiterschleife im Magnetfeld innerhalb einer Zeitspanne darstellt, unter dieser Voraussetzung erst eine Induktionsspannung im Magnetischen Feld auftreten kann!
1) Versuchsaufbau
In diesem Artikel soll ein in Abb. 1 aufgezeigter zentraler Versuchsaufbau gelten:
Hierin zu sehen ist eine , welche um eine drehbar gelagert sein möge. Die durch die Leiterschleife ausgebildete Fläche wird stehts vollständig von dem durchströmt. Die abgebildete Leiterschleife sei hier um ca
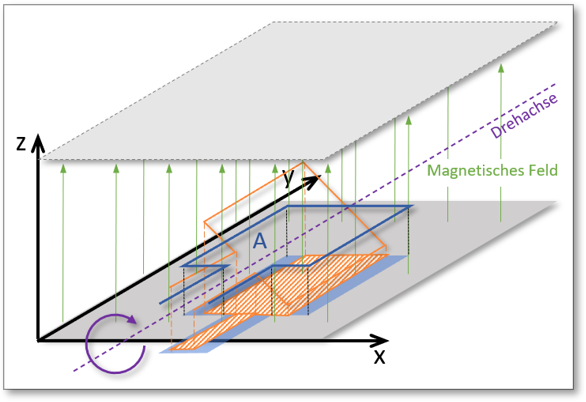
Abb. 1: Drehbar gelagerte Leiterschleife im Magnetischen Feld B
Mit Abb. 2 vergrößern wir den Bereich um die drehbare Leiterschleife und lenken unseren Fokus auf die durch die Leiterschleifen aufgespannten Flächen A, hierbei können wir zweierlei erkennen:
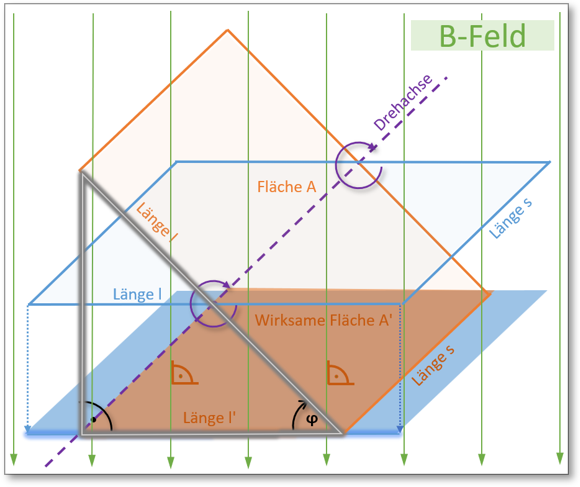
Abb. 2: Leiterschleife und Darstellung der wirksamen Fläche A'
Die nicht gedrehte Leiterschleife wird (zum Zeitpunkt ) senkrecht vom Magnetfeld durchströmt. Nachdem hiermit gilt , geht auch deren aufgespannte Fläche vollständig in die Berechnung unserer Induktionspannung ein.
Die (zum Zeitpunkt um ) gedrehte Leiterschleife wird nicht mehr senkrecht vom Magnetfeld durchströmt. Durch senkrechte Projektion können wir allerdings jenen Längenanteil ermitteln, für welchen wiederum gilt. Ersichtlich folgt daraus . Bei gleichbleibender Länge können wir nun berechnen: , die für die Ermittlung der Induktionsspannung wirksame Fläche . Es gilt damit . Folglich wird die gedrehte orange Leiterschleife also eine kleinere Induktionsspannung hervorrufen!
2) Ermittlung der wirksamen Fläche per Winkelfunktion
Unter Zuhilfenahme der Trigonometrie (wörtlich Dreiecksvermessung) können Beziehungen zwischen Seiten und Winkel von Dreiecken untersucht werden. Insbesondere auch für rechtwinklige Dreiecke wurden sogenannte trigonometrische Funktionen, auch Winkelfunktionen genannt, aufgestellt (zur Wiederholungen siehe LINK).
In Abb. 2 können wir ein ebensolches markiertes rechtwinkliges Dreieck ausmachen.
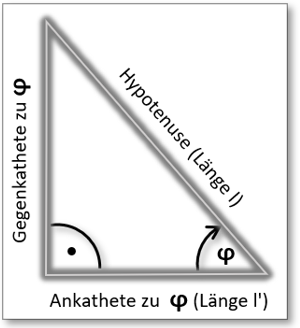
Abb. 3: Die Kosinus-Winkelfunktion
Allgemeingültig für
3) Weiterführung des Versuches
Ausgehend von unserer bisher gezeigten Drehung von , wollen wir nun in den nachfolgenden Abb. 4ff unsere Leiterschleife eine vollständige Drehung von in -Schritten vollziehen lassen.
Wir erkennen hierbei, dass die senkrechte Projektion der Leiterschleife nach unten eine sich verändernde Fläche ergibt. Jene der wirksamen Fläche , welche wie eben gezeigt direkten Einfluß auf unsere Induktionsspannung hat.
Wie nun können wir hieraus einen vollständigen Kosinusverlauf konstruieren?
4) Konstruktion eines Kosinusverlaufes
Grundlegendes zum Verständnis
Der Vollwinkel eines Kreises beträgt , dieser wiederum entspricht rad (für Radiant). Ein Radiant ist ein Winkelmaß, bei welchem der Winkel (hier der Vollkreis) durch die Länge des Kreisbogens (auch Bogenmaß genannt) mit angegeben wird. ( 3,14 für Pi)
Die Periodendauer für eine komplette Drehung () ist als definiert.
Die Winkelgeschwindigkeit ist definiert mit: und soll für unseren Versuch konstant sein. ( für klein Omega).
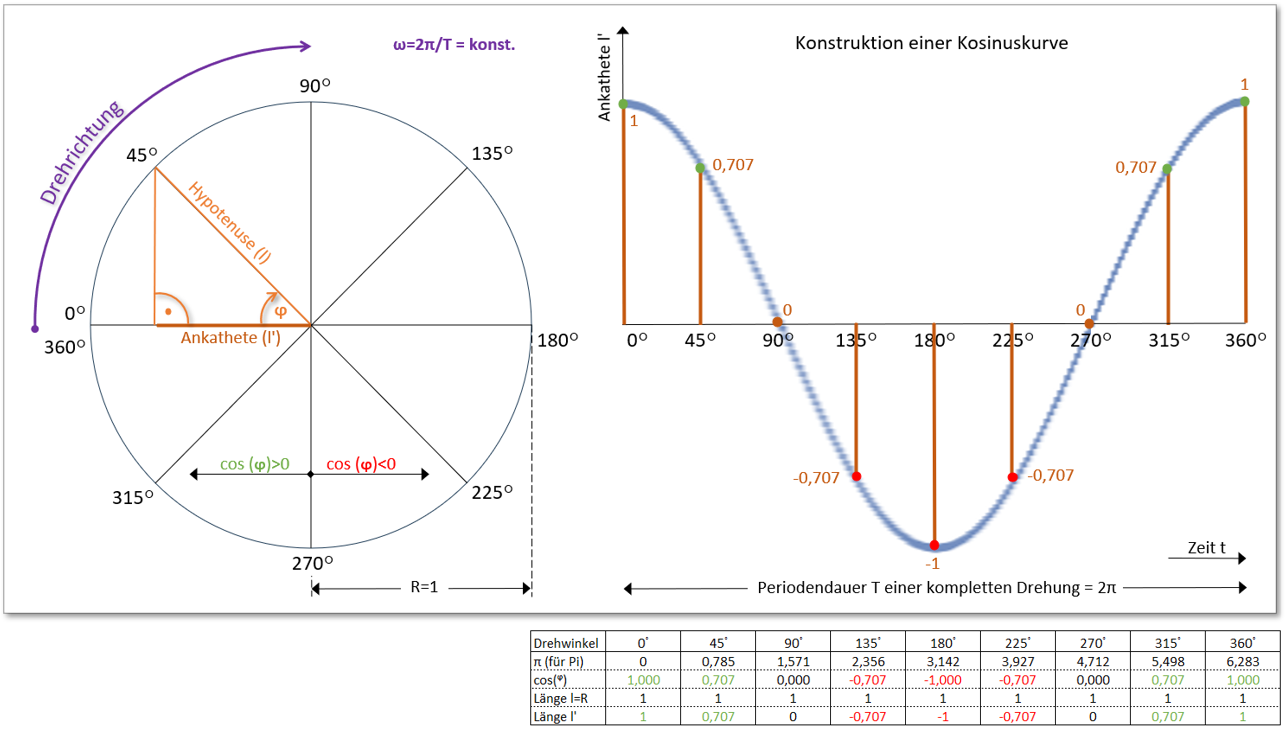
Abb. 5: Konstruktion eines Kosinusverlaufes aus Drehung im Vollkreis
5) Zusammenfassende Erkenntnis
Mit unserer o.g. abgeleiteten Formel . . .
und
. . . erkennen wir zusammenfassend folgendes:
Durch Drehung einer Leiterschleife, trifft das Magnetische Feld nicht mehr zwangsläufig senkrecht auf die konstante Fläche (Ausnahme oder ).
Für all jene Fälle muß die wirksame Fläche (jener Flächenanteil für diesen gilt ) unter Zuhilfenahme des berechnet werden.
stellt demnach eine Art Korrekturfaktor dar, welcher zwischen pendelt und die Fläche hin zu Fläche entsprechend korrigiert.
Nachdem das Magnetische Feld als auch die Fläche konstant sind, beeinflußt der Drehwinkel und damit auch zentral und ausschließlich die Induktionsspannung .
Im vorliegenden Versuch der Drehung einer Leiterschleife im Magnetischen Feld entsteht eine Induktionsspannung nur dadurch, sich die Fläche aufgrund der Drehung in ihrer Wirkung permanent ändert. Dies ausgedrückt durch deren wirksame Fläche :
und damit ebenso der Faktor
6) Ergebnis
Vielfache volle Umdrehungen einer Leiterschleife im Magnetfeld führen durch Aneinanderreihung der durch die -Funktion erzeugten Induktionsspannung zu einem in Summe sinusförmigen Verlauf (siehe Abb. 6).
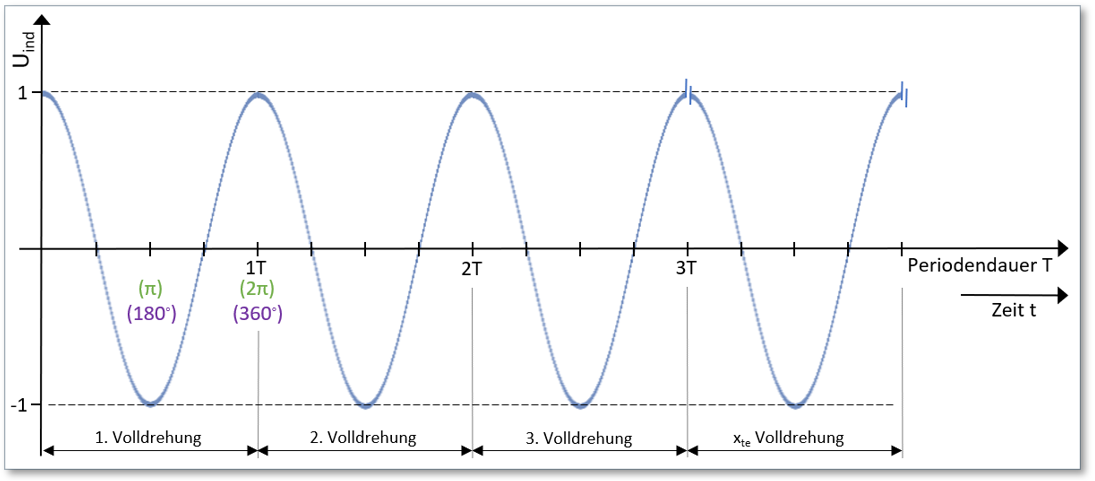
Abb. 6: Sinusförmige Induktionsspannung
Dies wiederum ist in der praktischen Anwendung die technische Basis für jeden Generator, z.B. dem Dynamo deines Fahrrades. Hierzu später noch mehr.
Quellen
- https://pixabay.com
- Bilder in Eigenkonstruktion
