Testaufgaben 1. Stunde

Eintragen der gegeben Werte in die beiden Darstellungsformen

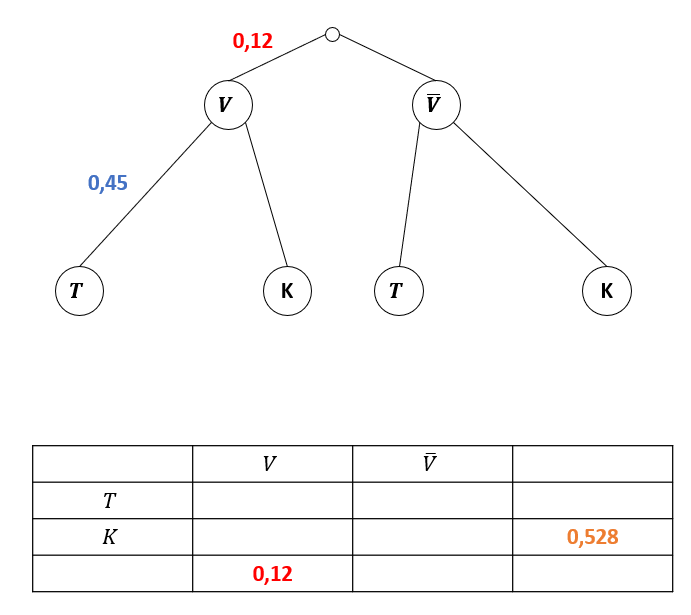
Zeichne eine leere Vierfeldertafel und ein leeres Baumdiagramm. Laut Angabe sind die Buchstaben $V,\overline{V},T$ und $K$ zu verwenden. Trage die gegebenen Werte ein:

Woher kommen die Zahlen?

• Die 12% sind $P\left(V\right)=\mathrm{0,12}$ und können deshalb sowohl in der unteren Zeile der Vierfeldertafel als auch auf erster Stufe des Baumdiagramms eingetragen werden

• Die 45% sind die bedingte Wahrscheinlichkeit $P_V\left(T\right)=\mathrm{0,45}$. Da in deinem Baumdiagramm V auf erster Stufe steht, kannst du die bedingte Wahrscheinlichkeit dort auf 2. Stufe ergänzen.

• Die Wahrscheinlichkeit $P\left(K\right)=\mathrm{0,528}$ kann nur in der Vierfeldertafel eingetragen werden, da sie im Baumdiagramm nicht vorkommt.

Lücken durch Zusammenhänge schließen

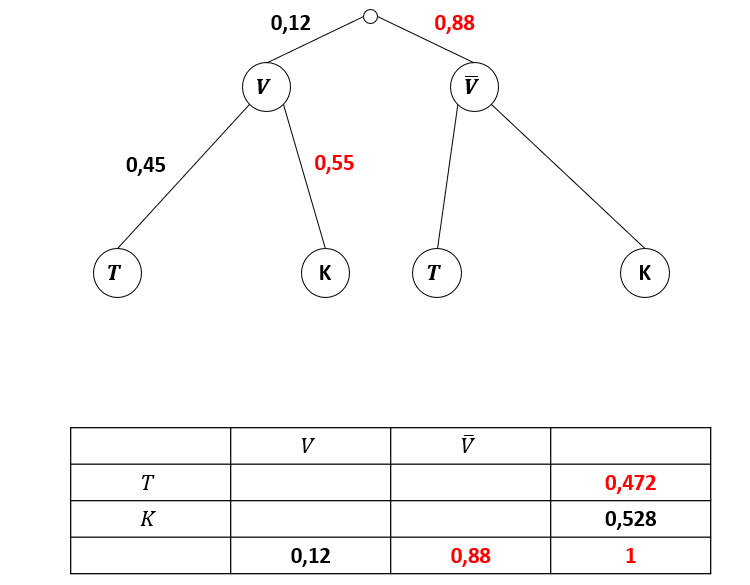
Nutze die folgenden Zusammenhänge, um einige Zahlen zu ergänzen:

• Die Summe aller Wahrscheinlichkeiten, die von einem Knoten im Baumdiagramm ausgehen, ist 1.

• In der Vierfeldertafel ist unten rechts ebenfalls $P\left(\mathrm{\Omega }\right)=1$.

Pfadregel

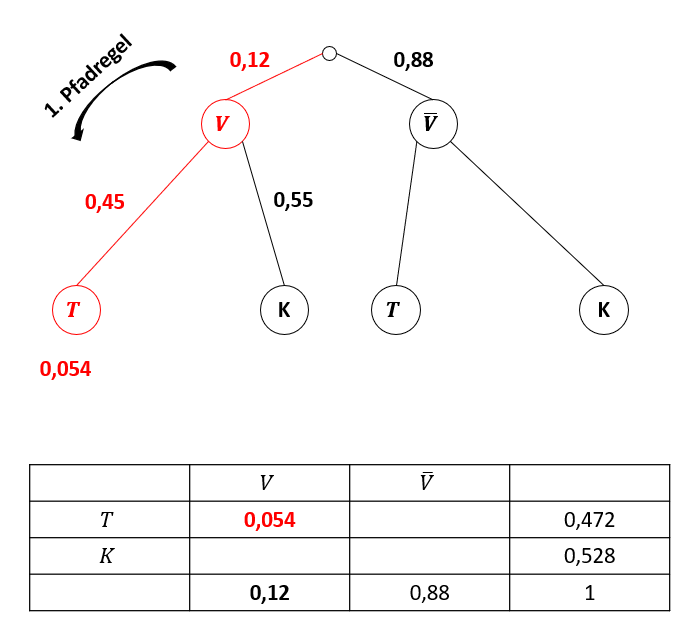
Verwende die erste Pfadregel, um $P(V\cap T)$ zu berechnen:

$P(V\cap T)=P\left(V\right)\cdot P_V\left(T\right)=\mathrm{0,12}\cdot \mathrm{0,45}=\mathrm{0,054}$

Diese Wahrscheinlichkeit kannst du sowohl im Baumdiagramm als auch in der Vierfeldertafel markieren:

Vierfeldertafel vervollständigen

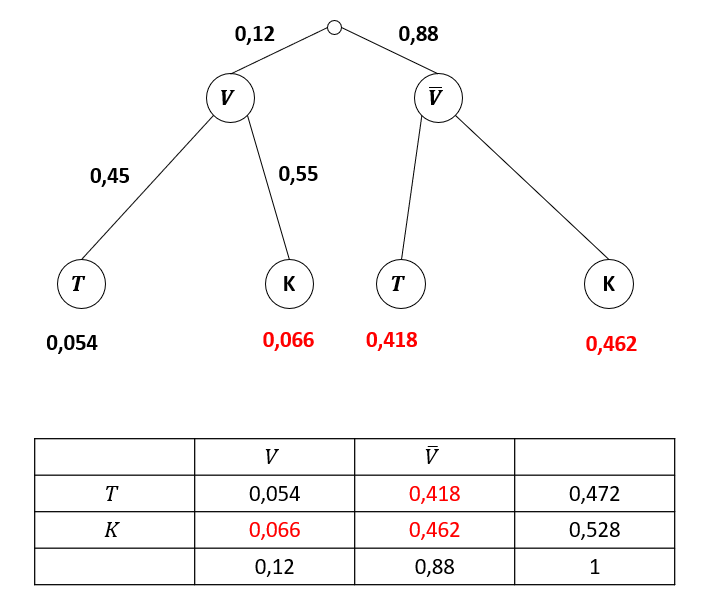
Die übrigen drei Felder in der Vierfeldertafel kannst du jetzt durch Subtrahieren berechnen und anschließend die Werte in das Baumdiagramm übertragen:

Bedingte Wahrscheinlichkeiten in Baumdiagramm ergänzen

Verwende nun die 1. Pfadregel rückwärts, um die bedingte Wahrscheinlichkeit zu bestimmen:

$P_{\overline{V}}\left(T\right)=\frac{P(\overline{V}\cap T)}{P\left(\overline{V}\right)}=\frac{\mathrm{0,418}}{\mathrm{0,88}}=\mathrm{0,475}$

und somit $P_{\overline{V}}\left(K\right)=1-\mathrm{0,475}=\mathrm{0,525}$

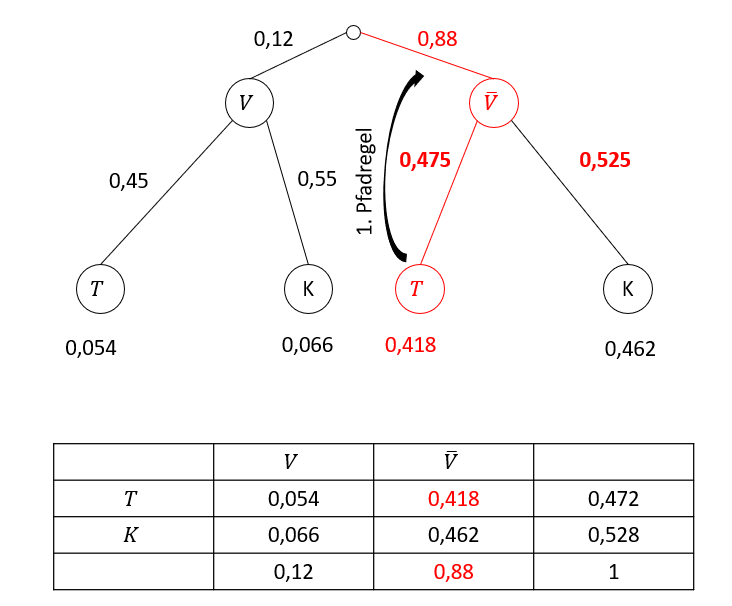
Im Baumdiagramm und in der Vierfeldertafel siehst du jeweils die Werte, die zur Berechnung der bedingten Wahrscheinlichkeit verwendet werden.

Im Baumdiagramm führst du die 1. Pfadregel rückwärts aus. Anstatt also zu multiplizieren, um die gesamte Pfadwahrscheinlichkeit zu erhalten, dividierst du.

In der Vierfeldertafel gibt es parallelen zur Berechnung von relativen Häufigkeiten bzw. Wahrscheinlichkeiten. Du teilst nicht mehr durch die 100%, sondern schränkst die Grundmenge auf die 88% ein.

Beantwortung der Frage

Gesucht war der Anteil der Personen, die aus Tierwohl-Gründen auf Fleisch verzichten würden, wenn bekannt ist, dass sie aktuell noch Fleisch essen.

Es geht also um die bedingte Wahrscheinlichkeit $P_{\overline{V}}\left(T\right)$.

Aus dem Baum entnimmst du $P_{\overline{V}}\left(T\right)=\mathrm{0,475}=\mathrm{47,5}\%$