Tangente und Normale

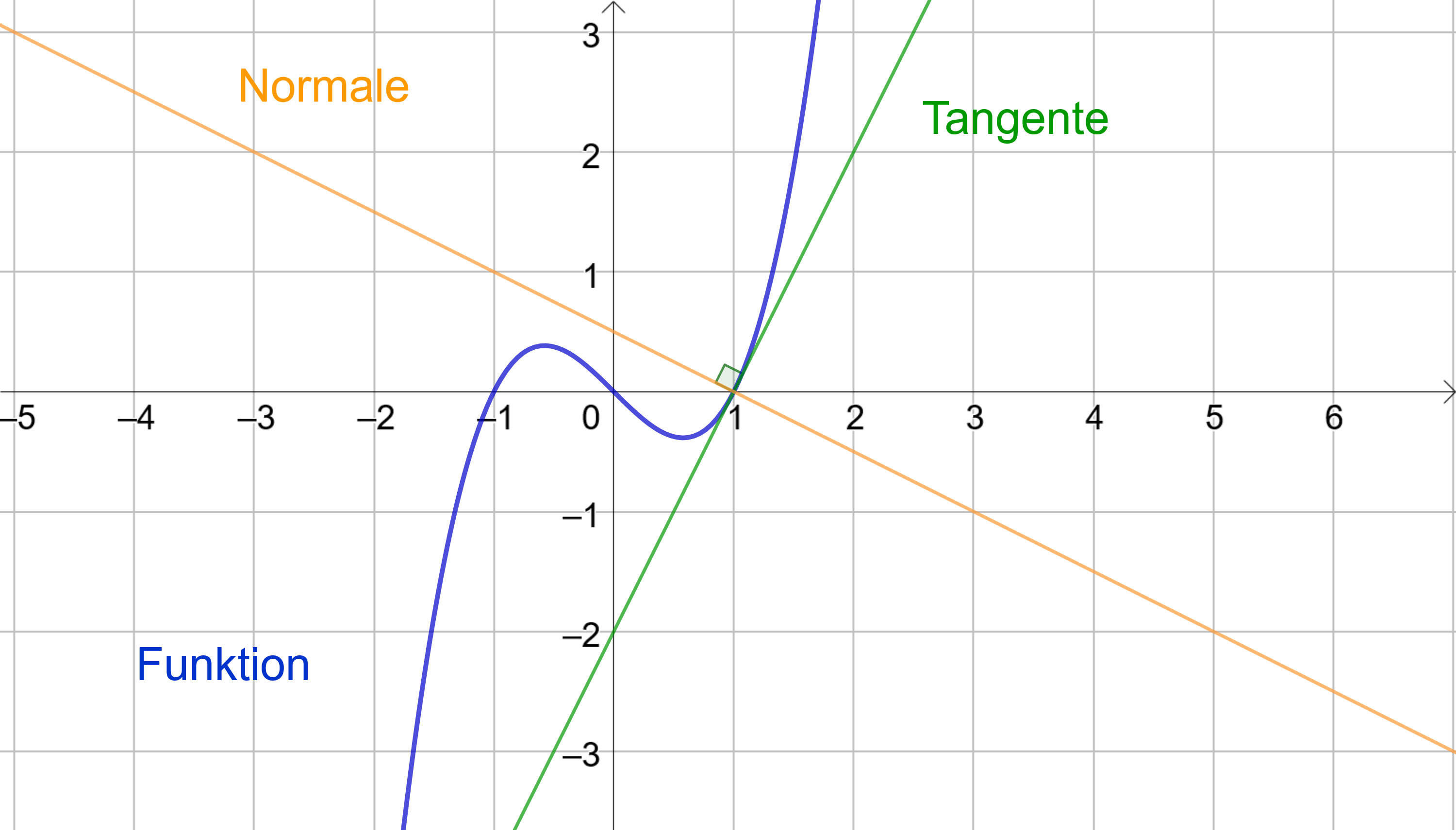
Eine Tangente ist eine Gerade, die einen Funktionsgraphen an einer Stelle berührt (nicht schneidet). Die dazugehörige Normale schneidet die Tangente und somit auch den Graphen der Funktion senkrecht an der gleichen Stelle.

Benötigtes Vorwissen

Du solltest einen Funktionsterm ableiten können und Steigungen an bestimmten Stellen bestimmen können.
Der Term einer linearen Funktion samt deren Steigung $m$ und y-Achsenabschnitt $b$ sollten bekannt sein.

Bestimmen einer Tangentengleichung

Ist nach einer Tangente gefragt, die den Graphen einer Funktion $f$ an einer Stelle berühren soll, ist die Aufgabe deren Funktionsgleichung $f_{t} (x)$ aufzustellen. Die Funktion bekommt den Namen $f_{t}$ , was für Tangente stehen soll. Da ihr Schaubild eine Gerade ist, wird sie durch eine lineare Funktion der Form

f_{t} (x) = m x + b

beschrieben. Hier ist $m$ wie üblich die Steigung und $b$ der y-Achsenabschnitt.

Da die Tangente einen Graphen berührt, besitzt sie an dieser Stelle die gleiche Steigung wie die Funktion $f$ . Somit kann die Steigung $m$ anhand der ersten Ableitung der Funktion bestimmt werden, wie das folgende Beispiel zeigt. Der y-Achsenabschnitt wird zuletzt durch eine Gleichung bestimmt, die der Punkt liefert, durch den die Tangente verläuft.

Beispiel zur Tangentenbestimmung

Eine Funktion $f (x) = x^{3} - x$ wird an der Stelle $x_{0} = 1$ tangiert (von einer Tangente berührt). Die Steigung der Tangente wird so berechnet:

$f (x)$	$=$	$x^{3} - x$
	↓	ableiten
$f^{'} (x)$	$=$	$3 x^{2} - 1$	$x_{0} = 1$
$f^{'} (1)$	$=$	$3 \cdot 1 - 1$
	$=$	$2$
$m$	$=$	$2$

Die Tangente besitzt nun die Form:

f_{t} (x) = 2 x + b

Um $b$ zu berechnen braucht es eine weitere Information, die uns in Form eines Punktes geliefert wird. Da Funktion $f$ hat an der Stelle $x_{0} = 1$ den Funktionswert

f (1) = 1^{3} - 1 = 0

Die Funktion und somit auch die Tangente verlaufen durch den Punkt $P (1 | 0)$ . Setzt man diese Information in die Tangentengleichung ein erhält man die Gleichung:

$0$	$=$	$2 \cdot 1 + b$	$- 2$
$- 2$	$=$	$b$

Die Tangentengleichung ist also:

f_{t} (x) = 2 x - 2

Tangentenformel

Da das Aufstellen der Tangentengleichung immer gleich funktioniert, kann der Ablauf sogar in eine Formel gepackt werden:

f_{t} (t) = f^{'} (x_{0}) (x - x_{0}) + f (x_{0})

Das Schema zur Berechnung der Tangente ist schrittweise abzuarbeiten.

Beispiel zur Tangentenformel

Die Funktion $f (x) = - 2 x^{2} + 3 x - 1$ wird in $x_{0} = 2$ von einer Tangente berührt. Wir bestimmen deren Funktionsterm $f_{t} (x)$ .

Allgemein	Beispiel
$f (x_{0})$ berechnen	$f (2) = - 2 \cdot 2^{2} + 3 \cdot 2 - 1 = - 3$
$f^{'} (x)$ bestimmen	$f^{'} (x) = - 4 x + 3$
$f^{'} (x_{0})$ berechnen	$f^{'} (2) = - 4 \cdot 2 + 3 = - 5$
$f (x_{0}), f^{'} (x_{0}), x_{0}$ in Formel einsetzen	$f_{t} (x) = - 5 (x - 2) + (- 3)$
Funktionsterm vereinfachen	$f_{t} (x) = - 5 x + 10 - 3 = - 5 x + 7$

Der Funktionsterm der Tangente ist also:

f_{t} (x) = - 5 x + 7

Bestimmen der Normalensteigung $m_{n}$

Ausgehend von einer Tangente ist es zur Normalen nicht weit. Da diese beiden Geraden senkrecht aufeinanderstehen erfüllen ihre Steigungen $m_{t}$ und $m_{n}$ folgende Gleichung:

m_{n} \cdot m_{t} = - 1

Die Steigung der Normalen ergibt sich mithilfe $m_{t}$ einfach durch:

m_{n} = - \frac{1}{m_{t}}

Beispiele zur Bestimmung von $m_{n}$

Steigung der Tangente	Steigung der Normale
$3$	$- \frac{1}{3}$
$- 7$	$- \frac{1}{7}$
$\frac{1}{2}$	$- 2_{}$
$- \frac{2}{5}$	$\frac{2}{5}$

Die Normalengleichung lautet damit:

f_{n} (x) = - \frac{1}{m_{t}} + b

Der y-Achsenabschnitt $b$ wird genau wie im Fall der Tangente mithilfe des Punktes berechnet, durch den die Normale verläuft.

Normalenformel

Das Aufstellen der Normalengleichung ist genauso systematisch wie das Bestimmen einer Tangente und kann mit der Formel

f_{n} (x) = - \frac{1}{f ′ (x_{0})} (x - x_{0}) + f (x_{0})^{}

vorgenommen werden.

Beispiel zur Normalenformel

Die Funktion $f (x) = 2 x^{3} + x^{2}$ wird in $x_{0} = - 1$ von einer Normalen geschnitten. Wir bestimmen deren Funktionsterm $f_{n} (x)$ .

Allgemein	Beispiel
$f (x_{0})$ berechnen	$f (- 1) = 2 \cdot (- 1)^{3} + (- 1)^{2} = - 1$
$f^{'} (x)$ bestimmen	$f^{'} (x) = 6 x^{2} + 2 x$
$f^{'} (x_{0})$ berechnen	$f^{'} (- 1) = 6 \cdot (- 1)^{2} + 2 \cdot (- 1) = 4$
$f (x_{0}), f^{'} (x_{0}), x_{0}$ in Formel einsetzen	$f_{n} (x) = - \frac{1}{4} (x - (- 1)) + (- 1)$
Funktionsterm vereinfachen	$f_{n} (x) = - \frac{1}{4} x - \frac{1}{4} - 1 = - \frac{1}{4} x - \frac{5}{4}$

Der Funktionsterm der Normalen ist damit:

f_{n} (x) = - \frac{1}{4} x - \frac{5}{4}

Übungsaufgaben

Laden

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org