Lagebeziehung Punkt-Ebene (Inzidenz)

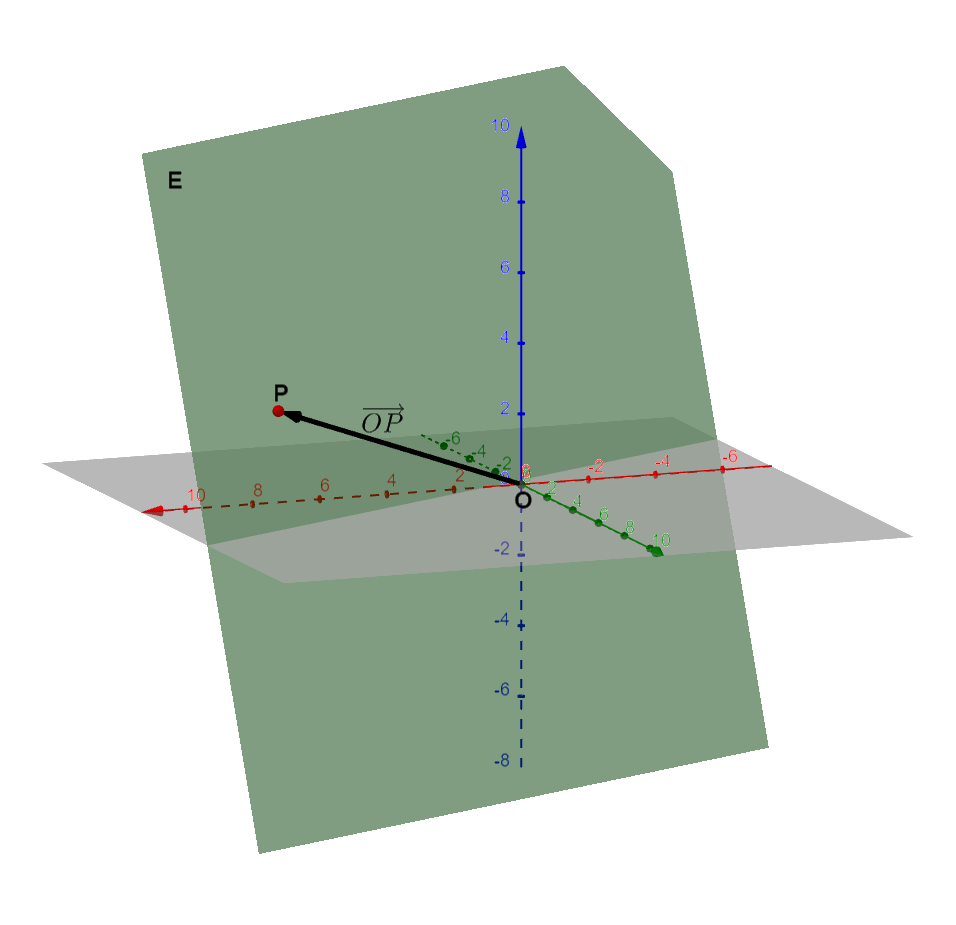
Ebenenformen

1. Parameterform

Die Ebenengleichung ist in der folgenden Form gegeben:

$E:\overrightarrow{X}=\overrightarrow{OA}+r\cdot \overrightarrow{u}+s\cdot \overrightarrow{v}$

Dabei ist $A$ der Aufpunkt und $\overrightarrow{u}$ und $\overrightarrow{v}$ sind die Richtungsvektoren der Ebene.

Führe eine Punktprobe durch:

Setze für $\overrightarrow{X}$ den Vektor $\overrightarrow{OP}$ ein:

$\overrightarrow{OP}=\overrightarrow{OA}+r\cdot \overrightarrow{u}+s\cdot \overrightarrow{v}$

Du hast ein Gleichungssystem mit drei Gleichungen und zwei Unbekannten erhalten.

Hat das Gleichungssystem eine Lösung, dann liegt der Punkt $P$ in der Ebene. Hat das Gleichungssystem keine Lösung, dann liegt der Punkt $P$ nicht in der Ebene.

Beispiel Punkt $P$ liegt in der Ebene $E$ (Parameterform)

Gegeben sind die Parameterform der Ebenengleichung $E$ und der Punkt $P$:

$E:\overrightarrow{X}=\left(\begin{array}{c}1\\ 2\\ 2\end{array}\right)+r\cdot \left(\begin{array}{c}2\\ -1\\ 2\end{array}\right)+s\cdot \left(\begin{array}{c}-3\\ -1\\ -1\end{array}\right)$und $P(9|3|6)$

Führe eine Punktprobe durch:

Setze für $\overrightarrow{X}$ den Vektor $\overrightarrow{OP}$ ein:

$\left(\begin{array}{c}9\\ 3\\ 6\end{array}\right)=\left(\begin{array}{c}1\\ 2\\ 2\end{array}\right)+r\cdot \left(\begin{array}{c}2\\ -1\\ 2\end{array}\right)+s\cdot \left(\begin{array}{c}-3\\ -1\\ -1\end{array}\right)\Rightarrow \left(\begin{array}{c}8\\ 1\\ 4\end{array}\right)=r\cdot \left(\begin{array}{c}2\\ -1\\ 2\end{array}\right)+s\cdot \left(\begin{array}{c}-3\\ -1\\ -1\end{array}\right)$

Du hast ein Gleichungssystem mit drei Gleichungen und zwei Unbekannten erhalten.

$\begin{array}{rrrrrcrr}& (\mathrm{I}):& & 8& =& 2\cdot r& -& 3\cdot s\\ & (\mathrm{I}\mathrm{I}):& & 1& =& -1\cdot r& -& 1\cdot s\\ & (\mathrm{I}\mathrm{I}\mathrm{I}):& & 4& =& 2\cdot r& -& 1\cdot s\end{array}$

Dieses Gleichungssystem kannst du z.B. mit dem Additionsverfahren lösen.

Rechne z.B. $(\mathrm{I})-(\mathrm{I}\mathrm{I}\mathrm{I}):4=-2s\Rightarrow s=-2$

Aus Gleichung $(\mathrm{I}\mathrm{I}\mathrm{I})$folgt: $4=2\cdot r-(-2)\Rightarrow r=1$

Probe in Gleichung $(\mathrm{I}\mathrm{I}):1=-1-(-2)=1✓$

Du hast bei der Lösung des Gleichungssystems die Werte $r=1$ und $s=-2$ erhalten.

Ergebnis: Das Gleichungssystem hat eine Lösung, d.h. der Punkt $P$ liegt in der Ebene $E$.

Beispiel Punkt $P$ liegt nicht in der Ebene $E$ (Parameterform)

Gegeben sind die Parameterform der Ebenengleichung $E$ und der Punkt $P$:

und $P(8|2|8)$. Führe eine Punktprobe durch. Setze für $\overrightarrow{X}$ den Vektor $\overrightarrow{OP}$ ein:

Du hast ein Gleichungssystem mit drei Gleichungen und zwei Unbekannten erhalten.

$\begin{array}{rrrrrcrr}& (\mathrm{I}):& & 7& =& 2\cdot r& +& 3\cdot s\\ & (\mathrm{I}\mathrm{I}):& & 0& =& -1\cdot r& +& 1\cdot s\\ & (\mathrm{I}\mathrm{I}\mathrm{I}):& & 6& =& 2\cdot r& +& 2\cdot s\end{array}$

Dieses Gleichungssystem kannst du z.B. mit dem Additionsverfahren lösen.

Rechne z.B. $(\mathrm{I})-(\mathrm{I}\mathrm{I}\mathrm{I}):1=s$

Aus Gleichung $(\mathrm{I}\mathrm{I})$folgt: $r=s\Rightarrow r=1$

Probe in Gleichung $(\mathrm{I}\mathrm{I}\mathrm{I}):6=2\cdot 1+2\cdot 1=4$$\Rightarrow 6\ne 4$

Damit hat das Gleichungssystem keine Lösung.

Ergebnis: Der Punkt $P$ liegt nicht in der Ebene $E$.

2. Normalenform

Die Ebenengleichung ist in der folgenden Form gegeben:

Führe eine Punktprobe durch:

Setze für $\overrightarrow{OX}$ den Vektor $\overrightarrow{OP}$ ein:

Berechne die Vektordifferenz und dann das Skalarprodukt.

Ist das Skalarprodukt gleich $0$, dann liegt der Punkt $P$ in der Ebene $E$. Ist das Skalarprodukt ungleich $0$, dann liegt der Punkt $P$ nicht in der Ebene $E$.

Beispiel Punkt $P$ liegt in der Ebene $E$ (Normalenform)

Gegeben sind die Normalenform der Ebenengleichung $E$ und der Punkt $P$:

und $P(3|2|1)$. Führe eine Punktprobe durch. Setze für $\overrightarrow{OX}$ den Vektor $\overrightarrow{OP}$ ein:

Berechne die Vektordifferenz:

Berechne das Skalarprodukt:

Ergebnis: Das Skalarprodukt ist gleich $0$, d.h. der Punkt $P$ liegt in der Ebene $E$.

Beispiel Punkt $P$ liegt nicht in der Ebene $E$ (Normalenform)

Gegeben sind die Normalenform der Ebenengleichung $E$ und der Punkt $P$:

$E:[\overrightarrow{OX}-\left(\begin{array}{c}-4\\ 2\\ 3\end{array}\right)]\circ \left(\begin{array}{c}1\\ -2\\ 3\end{array}\right)=0$ und $P(3|-2|4)$

Führe eine Punktprobe durch. Setze für $\overrightarrow{OX}$ den Vektor $\overrightarrow{OP}$ ein:

Berechne die Vektordifferenz:

Berechne das Skalarprodukt:

Ergebnis: Das Skalarprodukt ist ungleich $0$, d.h. der Punkt $P$ liegt nicht in der Ebene $E$.

3. Koordinatenform

Die Ebenengleichung ist in der folgenden Form gegeben:

$E:a{x}_1+b{x}_2+c{x}_3-d=0$

Führe eine Punktprobe durch. Setze die Koordinaten des Punktes $P$ in die Koordinatengleichung ein:

Ergibt sich eine wahre Aussage, dann liegt der Punkt $P$ in der Ebene $E$.

Ergibt sich eine falsche Aussage, dann liegt der Punkt $P$ nicht in der Ebene $E$.

Beispiel Punkt $P$ liegt in der Ebene $E$ (Koordinatenform)

Gegeben sind die Koordinatenform der Ebenengleichung $E$ und der Punkt $P$:

$E:3x_1-2x_2+4x_3=12$ und $P(4|2|1)$

Führe eine Punktprobe durch:

Setze die Koordinaten des Punktes $P$ in die Koordinatengleichung ein.

$3\cdot 4-2\cdot 2+4\cdot 1\stackrel{?}{=}12$

$12-4+4=12✓$

Du hast eine wahre Aussage erhalten, d.h. der Punkt $P$ liegt in der Ebene $E$.

Beispiel Punkt $P$ liegt nicht in der Ebene $E$ (Koordinatenform)

Gegeben sind die Koordinatenform der Ebenengleichung $E$ und der Punkt $P$:

$E:3x_1+4x_2-2x_3=8$ und $P(2|-2|-1)$

Führe eine Punktprobe durch. Setze die Koordinaten des Punktes $P$ in die Koordinatengleichung ein.

$3\cdot 2+4\cdot (-2)-2\cdot (-1)\stackrel{?}{=}8$

$6-8+2=0\Rightarrow 0\ne 8$

Du hast eine falsche Aussage erhalten, d.h. der Punkt $P$ liegt nicht in der Ebene $E$.