Normalform

Dieser Artikel befindet sich im Sandkasten und wurde daher nicht auf Korrektheit geprüft! Sieh dir gern den folgenden, geprüften Artikel auf serlo.org an, wenn du mehr zum Thema wissen möchtest: allgemeine Form und Scheitelform einer quadratischen Funktion

Erklärung: 

Die Normalform ist eine quadratische Funktion. Im Gegensatz zur Scheitelform kann man bei ihr den y-Achsenabschnitt direkt ablesen.

Die Formel lautet: 𝑓(𝑥) = 𝑎𝑥² + 𝑏𝑥 + 𝑐 

Aufstellung: 

1. Man benötigt den y-Achsenabschnitt (0/c) und zwei weitere gegebene Punkte

2. Einsetzten des y-Achsenabschnittes in die Normalform

3. Zwei gegebene Punkte in zwei Gleichungen einsetzen und die Variablen a und b berechnen

4. Anschließend in die Normalform einfügen 

Nullstellenberechnung:

Man kann mit der Normalform die Nullstellen berechnen. Dazu musst du als erstes y gleich null setzen. Anschließend errechnest du die x-Werte für die Nullstellen durch Wurzelziehen. Manchmal ist es nicht direkt möglich die Nullstellen so zu berechnen, dann muss man die pq-Formel anwenden.

Umwandlung in Scheitelform:

$f\left(x\right)=x^2+4x+6_{}$ |Quadratische Ergänzung  $=x^2+4x+2^2-2^2+6$ |in eine binomische Formel umwandeln

$=(x+2{)}^2-2^2+6$

$=(x+2{)}^2-4+6$

$=(x+2{)}^2+2$ |Scheitelpunkt ablesen

Scheitelpunkt: S=(2|2)

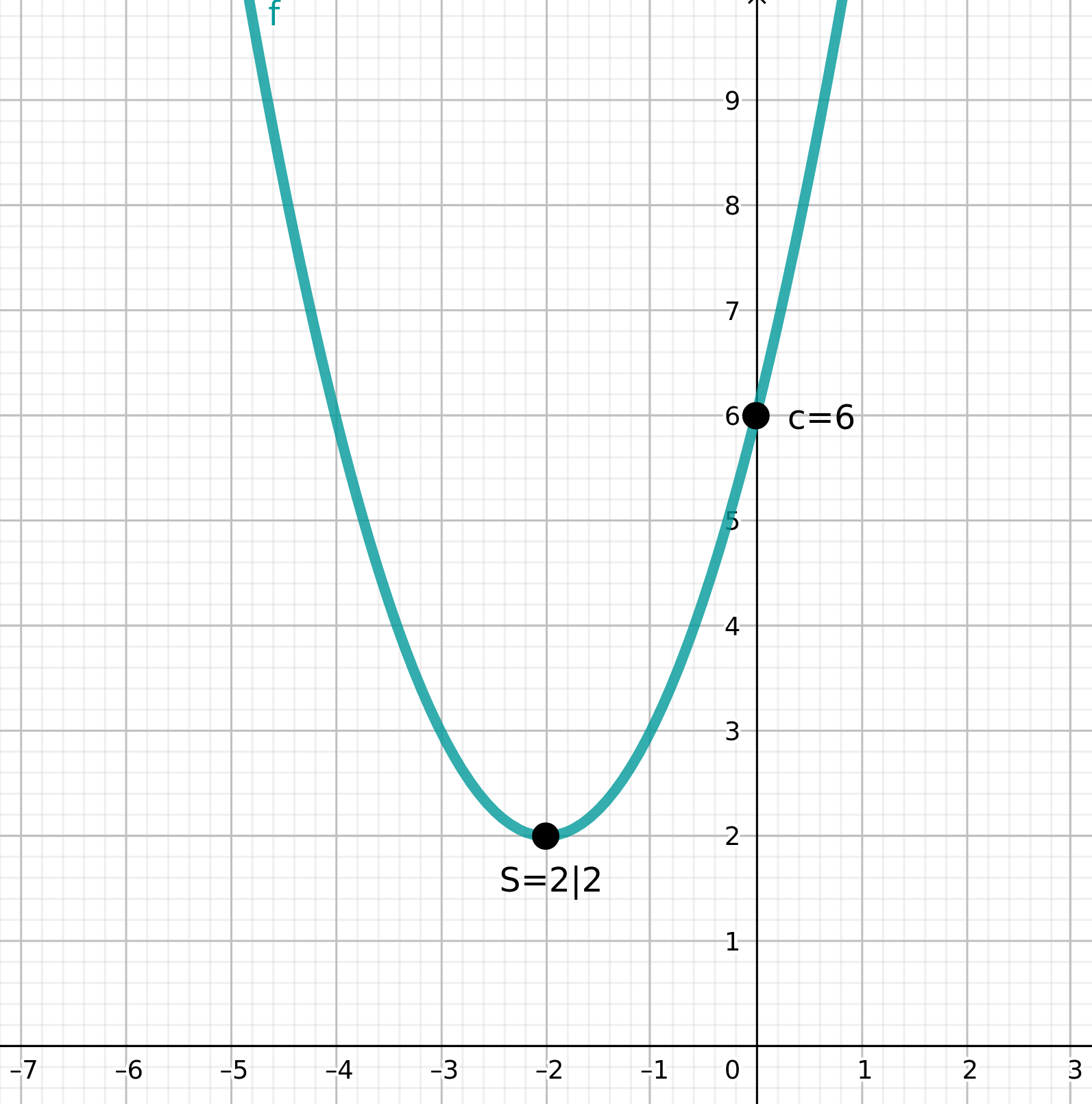
Video zur Umwandlung in die Scheitelform:

Beispielaufgaben:

1) Berechne die Nullstellen indem du die Gleichung 0 setzt:

a)

$f\left(x\right)=-x^2+25$

b)

$f\left(x\right)=-x^2+196$

2) Wandle in die Scheitelpunktform und bestimme den Scheitelpunkt:

a)

$f\left(x\right)=3x^2+18x+21_{}^{}$

b)

$f\left(x\right)=7x^2+28x+{35}_{}$