p-q Formel

Dieser Artikel befindet sich im Sandkasten und wurde daher nicht auf Korrektheit geprüft! Sieh dir gern den folgenden, geprüften Artikel auf serlo.org an, wenn du mehr zum Thema wissen möchtest: pq-Formel

Die p-q Formel wird verwendet, um bei quadratischen Gleichungen die Nullstellen auszurechnen.

Die Formel lautet:

x

=

- \frac{p}{2} \pm \sqrt{(\frac{p}{2})^{2} - q}

Man kann p und q aus der Gleichung entnehmen. Wenn man z.B die Gleichung (f(x)=x²+7x-8) hat, kann man die Zahl vor dem x als p und die alleinstehende Zahl als q nehmen. In diesem Fall: p=7 und q =-8. Wichtig ist hierbei, dass man ein alleinstehendes x² hat, ohne eine Zahl davor. Sonst müsste man es so umformen, sodass es alleinstehend ist. Nun setzen wir die Werte p und q in die Formel ein:

$x$	$=$	$- \frac{7}{2} \pm \sqrt{(\frac{7}{2})^{2} - (- 8)}$	$A u s r e c h n e n$
$x$	$=$	$- 3,5 \pm \sqrt{20,25}$	$A u r e c h n e n$

Jetzt muss man nur noch die Wurzel ziehen. Dabei erhält man dann: x=-3,5+4,5 oder x=-3,5-4,5

Also ist x=1 oder x=-8

Der Graph von x²+7x-8 :

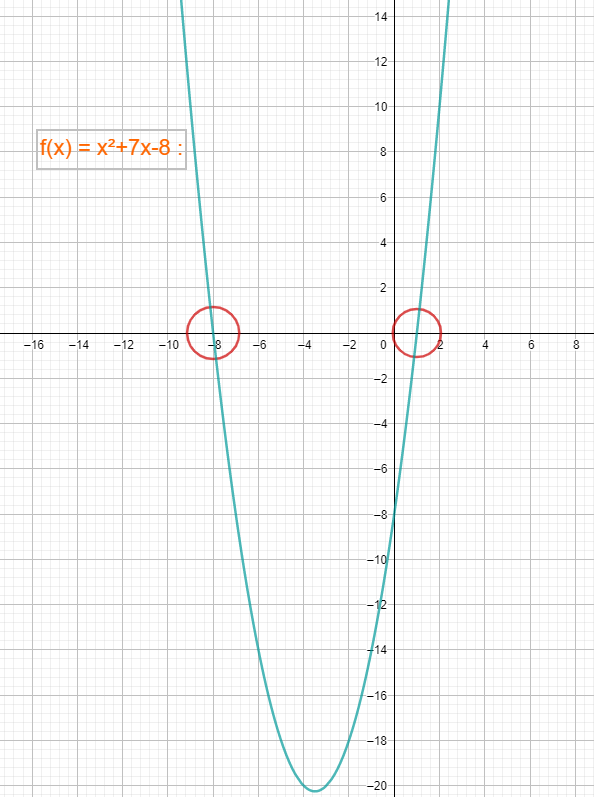
Wie man sehen kann durchschneidet der Graph die x-Achse

Wie man sehen kann, durschneidet die Parabel die x-Achse zwei mal, einmal bei -8 und einmal bei 1. Wie in der Lösung

Jetzt habe ich noch eine Übungsaufgabe für dich:

Berechne mit Hilfe der p-q Formel die beiden Schnittpunkte der Quadratischen Gleichung (f(x)=x²+6x-7)

2.Aufgabe: Berechne (f(x)=x²+4x-3)

x

=

- \frac{4}{2} \pm \sqrt{(\frac{4}{2})^{2} - (- 3)}

A u s r e c h n e n

x

=

- 2 \pm \sqrt{7}

x

=

- 2 \pm 2,64

x= -4,64 oder x=0,64

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org